Contingency Tables > Expected Frequency
What is Expected Frequency?
The expected frequency is a probability count that appears in contingency table calculations including the chi-square test. Expected frequencies also used to calculate standardized residuals, where the expected count is subtracted from the observed count in the numerator.
- Observed Frequencies are counts made from experimental data. In other words, you actually observe the data happening and take measurements. For example, you roll a die ten times and then count how many times each number is rolled. The count is made after the experiment.
- Expected Frequencies are counts calculated using probability theory. For example, before you roll a six-sided die, you calculate the probability of any one number being rolled as 1/6.
How to Calculate Expected Frequency by Hand
Expected frequencies are calculated for each cell in a contingency table. So if you have, say, 16 cells, you’ll need to perform the steps 16 times (one for each cell). The formula to calculate expected frequency is:
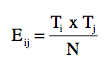
Tip: You can think of this equation more simply as (row total * column total) / grand total.
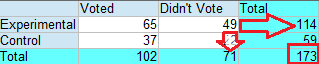
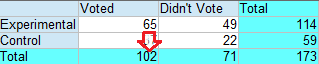
Sample question: What are the expected cell frequencies for the following table?
Step 1: Find Ti = total in the ith row. The first cell is in the first row (i=1), which has a total of 114.
Set this number aside for a moment.
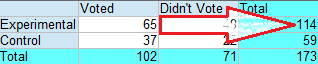
Step 2: Find Tj = total in the jth column. The first cell is in the first column (j=1), which has a total of 102.
Set this number aside for a moment.
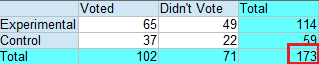
Step 3: Find N, or the total number of participants/items in the experiment. In a contingency table, this is usually done for you and is tallied up in the bottom right-hand corner. For this example, the total number of participants is 173.
Step 4: Insert the three numbers from Step 1, 2 , and 3 into the formula and solve:
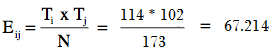
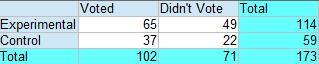
The expected cell frequency for cell 1 is 67.214.
Step 5: Repeat Steps 1 through 4 for each of the other cells.
The solutions for the remaining cells are:
- Cell 2 (top right) = (114 * 71) / /173 = 48.786

- Cell 3 (bottom left) = (59 * 102) / 173 = 34.786
- Cell 4 (bottom right) = (59 * 71) / 173 = 24.214.
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company