Regression Analysis > Weighted Least Squares
What is Weighted Least Squares?
Weighted Least Squares is an extension of Ordinary Least Squares regression. Non-negative constants (weights) are attached to data points. It is used when any of the following are true:
- Your data violates the assumption of homoscedasticity. In simple terms this means that your dependent variable should be clustered with similar variances, creating an even scatter pattern. If your data doesn’t have equal variances, you shouldn’t use OLS.
- You want to concentrate on certain areas (like low input value). OLS can’t “target” specific areas, while weighted least squares works well for this task. You may want to highlight specific areas in your study: ones that might be costly, expensive or painful to reproduce. By giving these areas bigger weights than others, you pull the analysis to that region’s data—. This focuses the analysis on the areas that matter (Shalizi, 2015).
- You’re running the procedure as part of logistic regression or some other nonlinear function. With any non-linear procedure, linear regression is usually not the most appropriate modeling tool unless you can group the data. In addition, the error terms in logistic regression are heteroscedastic, which means you can’t use OLS.
- You have any other situation where data points should not be treated equally. For example, you might give more preference to points you know have been precisely measured and a lower preference to points that are estimated.
Formula
Need help with a homework question? Check out our tutoring page!
Instead of minimizing the residual sum of squares (as seen in OLS):
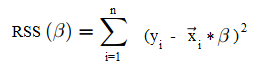
You minimize the weighted sum of squares:
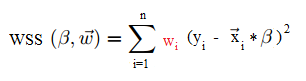
Although weighted least squares is treated as an extension of OLS, technically it’s the other way around: OLS is a special case of weighted least squares. With OLS, all the weights are equal to 1. Therefore, solving the WSS formula is similar to solving the OLS formula. You’re unlikely to actually solve this by hand though, as most decent stats software packages will have these built in.
Advantages and Disadvantages
Weighted least squares has several advantages over other methods, including:
- It’s well suited to extracting maximum information from small data sets.
- It is the only method that can be used for data points of varying quality.
Disadvantages include:
- It requires that you know exactly what the weights are. Estimating weights can have unpredictable results, especially when dealing with small samples. Therefore, the technique should only be used when your weight estimates are fairly precise. In practice, precision of weight estimates usually isn’t possible.
- Sensitivity to outliers is a problem. A rogue outlier given an inappropriate weight could dramatically skew your results.
Alternatives
WLS can only be used in the rare cases where you know what the weight estimates are for each data point. When heteroscedasticity is a problem, it’s far more common to run OLS instead, using a difference variance estimator. For example, White (1980) suggests replacing S2(X’X)-1 by X’DX. This is a consistent estimator for X’ΩX:
![]()
While White’s consistent estimator doesn’t require heteroscedasticity, it isn’t a very efficient strategy. However, if you don’t know the weights for your data, it may be your best choice. If you’d like a full explanation of how to implement White’s consistent estimator, you can read White’s original 1908 paper for free here.
References:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Engineering Stats. Handbook. Retrieved February 20, 2018 from: http://www.itl.nist.gov/div898/handbook/pmd/section1/pmd143.htm
Shalizi, C. (20150. Lecture 24–25: Weighted and Generalized Least Squares. Retrieved February 20, 2018 from: http://www.stat.cmu.edu/~cshalizi/mreg/15/lectures/24/lecture-24–25.pdf
White, Halbert (1980). “A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity”. Econometrica. 48 (4): 817–838. doi:10.2307/1912934