An error term in statistics is a value which represents how observed data differs from actual population data. It can also be a variable which represents how a given statistical model differs from reality. The error term is often written ε.
Examples of the Error Term in Statistics
In econometric theory, the classical normal linear regression model (CNLRM) involves finding the best fitting linear model for observed data that shows the relationship between two variables.
For example, let’s say you were running a study on the way the number of exams in a certain college affect the amount of red bull purchased from college vending machines. You could collect data which told you how many exams were given and how much red bull was purchased on a dozen or more days during the semester. This data can be plotted as a scatter plot, with exams (Ex) per given day on the x axis and red bull purchased (RB) per given day on the y axis. Then you would look for the line y = β0 + β1 x that best fit the data.
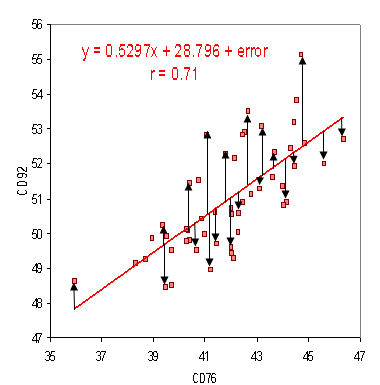
“Best fit” here means that the error term, the distance from each point to the line, is minimized. Since the relationship between variables is probably not completely linear and because there are other factors outside the scope of our study (sales on red bull, sales on other caffeine drinks, difficult physics homework sets, etc.) the graph of the probability distribution won’t actually go through all our data points. The distance between each point and the linear graph (shown as black arrows on the above graph) is our error term. So we can write our function as RB=β0 + β1 Ex + ε where β0 and β1 are constants and ε is an (non constant) error term.
Properties of the Error Term
The error term includes everything that separates your model from actual reality. This means that it will reflect nonlinearities, unpredictable effects, measurement errors, and omitted variables.
Errors and Residuals
Although the terms error and residual are often interchanged, there is an important formal difference. While an error term represents the way observed data differs from the actual population, a residual represents the way observed data differs from sample population data. This means that a residual is often much easier to quantify. Although an error is generally unobservable, a residual is observable.
The residual can be considered an estimate of the true error term.
Sources
What is Regression Analysis? Retrieved Nov 16.20 from http://www2.iona.edu/faculty/rjantzen/eco310/…/Studenmund_Ch01_v2.ppt
Causality in the Sciences