Consistent Estimator: Consistency Definition & Examples

Statistics Definitions > Consistent Estimator

What is a Consistent Estimator?

A consistent estimate has insignificant errors (variations) as sample sizes grow larger. More specifically, the probability that those errors will vary by more than a given amount approaches zero as the sample size increases. In other words, the more data you collect, a consistent estimator will be close to the real population parameter you’re trying to measure. The sample mean and sample variance are two well-known consistent estimators.

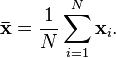
The idea of consistency can also be applied to model selection, where you consistently select the “true” model with the associated “true” parameters. For example, a goodness of fit test can also be used as measure of consistency. One popular goodness of fit test is the chi-square test, which works on the premise that expected values for your data fit a normal distribution. And if you have data from a time-series model, data consistency can be measured with an autoregressive model. Many other measures of consistency for fitting to data to models exist. Which method you use depends on what you want your data to measure. For example, do you think your data follows a linear trend, an exponential trend, or a specific trend like the one seen in this paper, which outlines a consistent estimator for disturbance components in financial models?

Origins

The term consistent estimator is short for “consistent sequence of estimators,” an idea found in convergence in probability. The basic idea is that you repeat the estimator’s results over and over again, with steadily increasing sample sizes. Eventually — assuming that your estimator is consistent — the sequence will converge on the true population parameter. This convergence is called a limit, which is a fundamental building block of calculus.

References:
Cramér, H. (1946). Mathematical methods of statistics” , Princeton Univ. Press I.A. Ibragimov, R.Z. [R.Z. Khas’minskii] Has’minskii, (1981) “Statistical estimation: asymptotic theory” , Springer. (Translated from Russian)
Levinsohn, J. & MacKie-Mason, J. (1989). A simple, cons. est. for disturbance components in financial models. National Bureau of Economic Research. Technical working paper No. 80. Retrieved January 7, 2017 from http://www.nber.org/papers/t0080.pdf.