An axis of rotation (also called an axis of revolution) is a line around which an object rotates. In calculus and physics, that line is usually imaginary. The radius of rotation is the length from the axis of rotation to the outer edge of the object being rotated.
Example of Axis of Rotation
A simple example is one axle or hinge that allows rotation, but not translation (movement). The following image shows a two-dimensional shape (a half bell) rotating around a single, vertical axis of rotation. If the shape travels 360 degrees, the result is a three-dimensional bell:
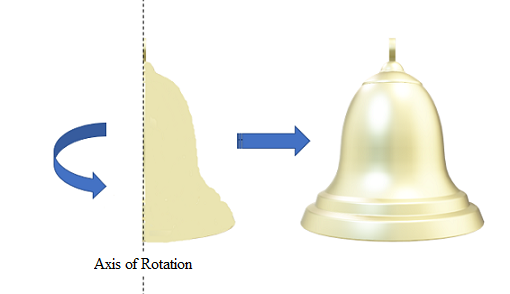
The final object (in this case, a bell) is called an object of revolution.
Radius of Rotation Example
The radius of rotation is a line segment that extends from the rotational axis to a point of interest on the outer edge.
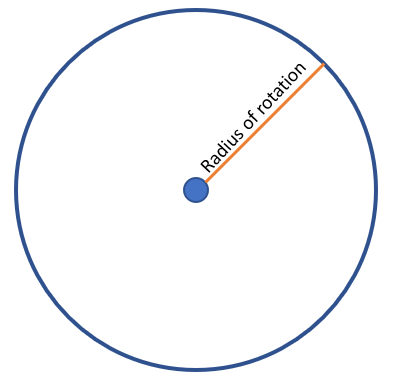
If you’re using the disc method, the radius of rotation is perpendicular (at right angles) to the axis of rotation.
Real Life Axis of Rotation Examples
1. Aviation
In aviation, “axis of rotation” refers to one of three axes, about which an airplane pitches, rolls, or yaws.
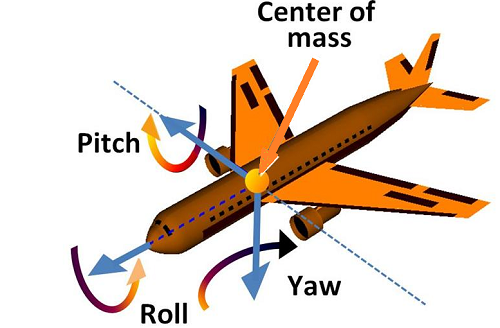
The three axes (shown in the above image with blue arrows) are:
- Lateral (pitch), controlled by the elevator,
- Longitudinal (roll), controlled by ailerons.
- Vertical (yaw), controlled by the rudder.
2. Earth’s Axis of Rotation

The Earth is tilted at an angle of 23.5° with respect to the Sun. The axis of rotation affects when the seasons happen;
- When the tilt is towards the Sun, it’s summer in the northern hemisphere and winter in the southern hemisphere.
- When the tilt is away from the Sun, it’s winter in the northern hemisphere and summer in the southern hemisphere.
The Earth’s tilt is much like a spinning top; It wobble’s as it orbits the Sun, creating a wobble effect.
Finding the Volume of a Solid of Revolution
The disc method or washer method are used to find the volume of objects of revolution in calculus. The disc method is used for solid objects, while the washer method is a modified disc method for objects with holes. More specifically:
- Use the disc method if:
- The axis of rotation is also the boundary (edge) of the two-dimensional object you’re rotating, and
- The cross sections (thin slices of the resulting solid) are taken perpendicular to the axis of rotation.
- Use the washer method if:
- The axis of rotation isn’t a boundary of the two-dimensional object, and
- The cross sections are taken perpendicular to the axis of rotation.
References
Smithsonian National Air and Space Museum. How Things Fly. Retrieved October 10, 2019 from: https://howthingsfly.si.edu/flight-dynamics/roll-pitch-and-yaw
Stewart, J. (2009). Calculus: Concepts and Contexts. Retrieved October 8, 2019 from: