The disc method (also called disc integration) is a way to find the volume of solids of revolution. You can use it for two dimensional rotated objects where the axis of rotation is also the boundary (edge) and cross sections (thin slices) are perpendicular to the axis of rotation. If the axis of rotation isn’t a boundary, use the washer method instead.
The formula for the disc method is:
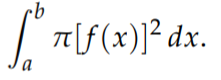
Disc Method: Example
Example question: Find the volume of the shape created when the equation x = 2 is revolved around the x-axis.
Solution:
Step 1: Draw the graph and rotate it around. If you have trouble visualizing this (which is very common!), try this great tool at Desmos.com. I used it to rotate the graph and create the following image of the object of revolution (shown in light blue):
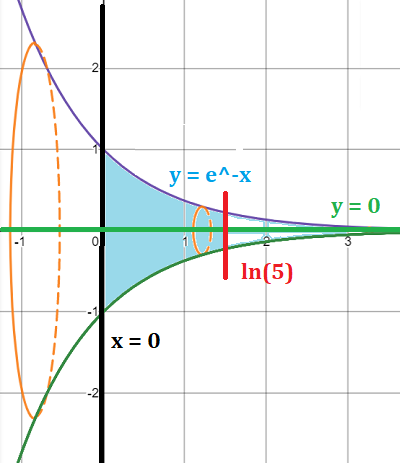
Step 2: Put the function into the integral formula. That’s the function that created the main “skin” of the shape: the boundary that you rotated. For this example, that’s y = e-x:
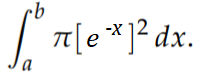
Step 3: Fill in the x-boundaries. The left boundary (a) for this example is 0; The right boundary (b) is ln(5):
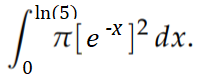
Step 4: Calculate the integral using the usual methods or a calculator. For this particular integral you’ll need a combination of u substitution and the power function rule for integrals. I used Symbolab’s calculator to get the solution:
12π/25
That’s it!
If you have difficulty visualizing rotations, the following video shows an example of how to visualize rotating a graph around the x-axis.