A Two Way ANOVA in SPSS has two independent variables. You would use a two way ANOVA when you have one measurement (scale) variable and two nominal variables. In the hypothetical example that follows, we are studying how brand of cleaner and water temperature (both nominal variables) affect cleanliness level (a scale variable).
Watch the video for the steps, including data entry, assumptions and reading the output:
Two Way ANOVA in SPSS: Running the Test
In this experiment, two brands of cleaner were compared to see how well they got kitchen pans clean. The brands were tested in two different water temperatures: hot and cold. Brand of cleaner is the independent variable and level of cleanliness the dependent variable. Water cleaner may also have an effect on how well the brands clean, so that is a second main effect under consideration. The interplay of Water Temperature and Brand may have an interaction effect and so is included in the analysis. There are many steps here: the short video above will walk you through the steps if you are unfamiliar with hypothesis testing in SPSS.
- Click Analyze, select General Linear Model, and then click Univariate.
- Click Your dependent variable (in this example, that’s Cleanliness), and then click the arrow by the “Dependent Variable box”.
- Click your main independent variable—the main focus of your experiment (for this example, that’s Brand of Cleaner, and then click the arrow for the Fixed Factor(s): box.
- Click your interaction variable (Water temperature in this example), and then click the arrow for Fixed Factor(s).
- Click EM Means box.
- Click your independent variable (“Brands”) in the Univariate Estimated Marginal Means window. Hold down Ctrl on your keyboard and then click Water and Brand*Water. Click the arrow to move all three to the Display Means for: box..
- Click Compare main effects.
- Click Continue.
- Click Options.
- Click Descriptive statistics and Homogeneity tests. You can change the alpha level here, but in this example, I’m going to leave it at the 5% level.
- Click Continue and then click OK.
Reading the Results in the Output Viewer Window
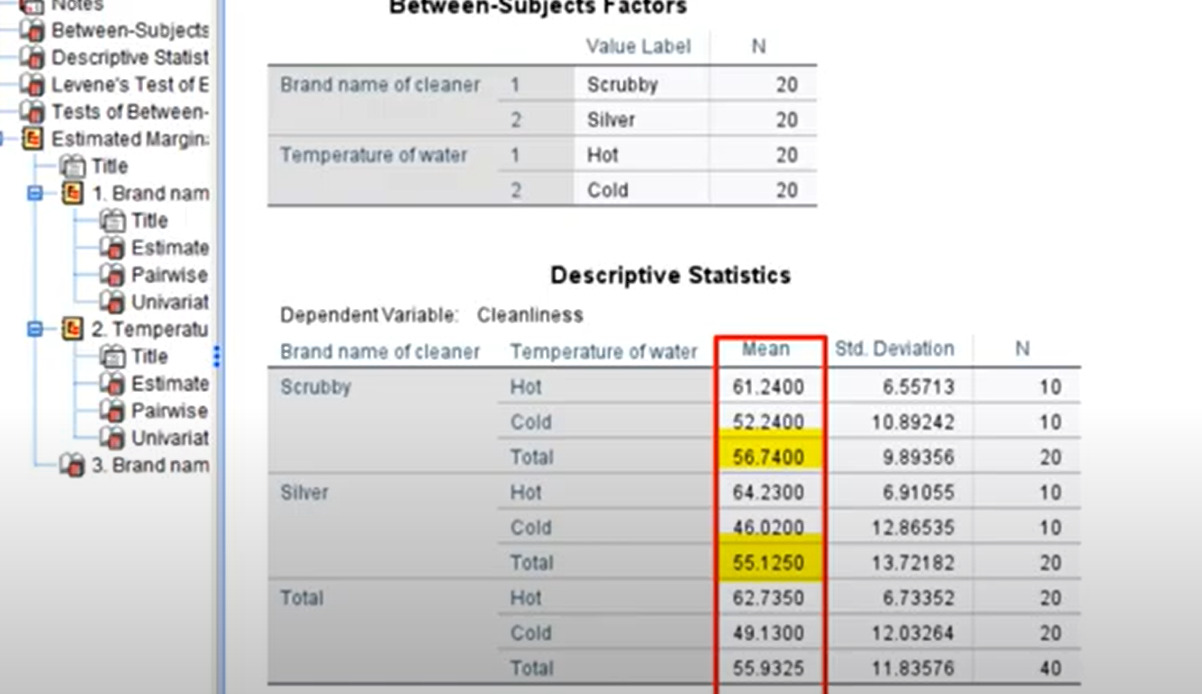
Base on the calculated means for the main effect, (shown in the above image), the research question becomes, “Is the difference between 56.74 and 55.125 statistically significant? in other words Is the main effect of Brand statistically significant?”
.
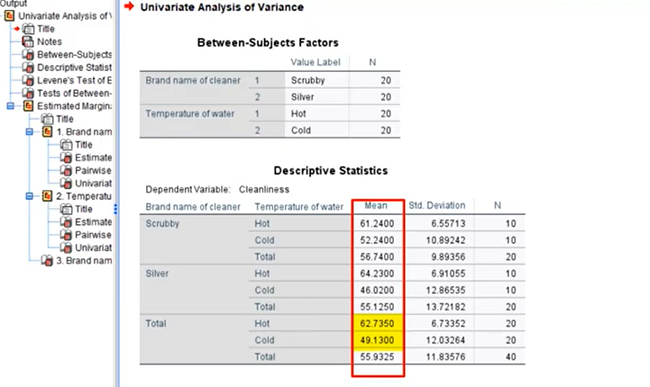
The main effects of water are also shown. We also want to know if there’s a significant difference between the means of 62.735 and 49.13.
The next section in the output shows the results for Levene’s Test.
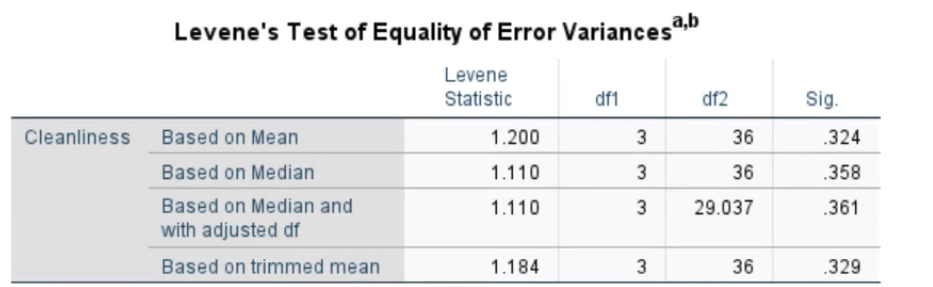
The null hypothesis for Levene’s test is one of equal error variances for all groups. Therefore, you do not want to reject the null hypothesis. All of our p-values are very large, about 30%, so the assumption of equal variance has been met. If you reject the null in this step, you should not continue reading results from the Two Way ANOVA in SPSS: they are invalid.
Now you can decide if you can reject or accept the null hypotheses for your main and interaction effects. This information is obtained from the Tests of Between-Subjects Effects box:
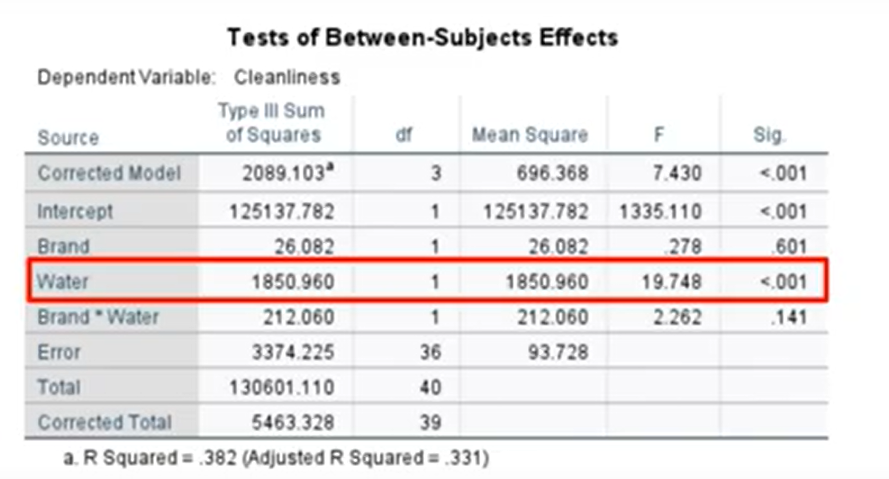
In this hypothetical example, we were testing three hypotheses:
- Differences in cleanliness levels by Brand: Not significant, with a p-value of .6 (third row down in the above image). As this is larger than our alpha level, any differences are due to chance.
- The main effect of water temperature on cleanliness: Statistically significant, at less than .001 (shown inside the red box in the above image).
- Interaction effects of brand and water were also not significant, as .141 is much larger than .05.
We can conclude that there is no significant difference between brand on the level of cleanliness. however, temperature of water makes a difference. If we go back to descriptive statistics, we see that hot water has a much higher mean and this was found to be significant. in other words, washing dishes in hot water makes a difference, no matter what brand you use.