Hypothesis Tests > Log-Rank Test
Contents:
1. What is the Log-Rank Test?
The log-rank test is a non-parametric hypothesis test to compare survival distributions from two samples. It is often used in clinical trials to compare survival experience for two groups of individuals. For example you might want to test if Drug A increases survival time compared to Drug B.
This test will tell you if there is a difference, but will not provide details about the size of the difference or provide you with a confidence interval.
Other tests for differences, like the two-sample t-test are not appropriate for this type of data, because the data is usually highly skewed.
Running the Test
The null hypothesis for the log-rank test is that there is no difference in survival probabilities between the two groups. The probability is calculated for some event, which could be death or another significant event.
The test compares estimates of the hazard functions of the two groups at each observed event time. The observed and expected number of events is calculated in one of the groups at each observed event time, then these results are added to get an overall summary for all points in time when an event happened. This test isn’t usually calculated by hand, because of the complexity of the calculations.
Assumptions
The assumptions for the log-rank test are:
- Censoring (which happens when you don’t know the exact survival time) must be unrelated to prognosis,
- Survival probabilities are equal for subjects recruited at any time in the study,
- The events happened at the specified time.
Variations
2. Weighted Log-Rank Test
The weighted Log-rank Test is used if you want to compare groups but want to give more importance (“weight”) to certain events.
While the log-rank test allows us to find the relative survival distribution for two samples, it assumes that every point in time has the same significance. It works best when hazards (threats to survival) are relatively constant over time, or proportional. The weighted log-rank test lets us make allowance for different times being more or less important. This makes it a very useful test for when hazards are not proportional; for instance, for when the odds of survival are much greater at the beginning of time and taper off at the end.
The weighted log-rank test is often used in clinical studies when a certain time or times is more relevant than others. For instance, in a clinical trial that tested an aggressive new cancer drug, one might want to focus more on short-term survival threats (caused by the drug’s potential toxicity) rather than on the long term possibility of getting well.
A conservative treatment, on the other hand, may take a while to actually make any difference to the participants of a study. In that case, we’d want to weight heavier for later time.
Choosing Weights for the Weighted Log-Rank Test
Weights should be chosen based on prior information you have on your research topic, and not on the survival curves. You’ll want to set your weights when designing your experiment, not after looking at your data set. If you choose weights based on your data set or survival curves, you risk circular reasoning in your results.
The formula for the weighted test is given by
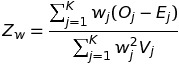
Here Oj-Ej is a measure of how the hazards differ per time j. The weighting is given by the wj; non-negative numbers that defines how important that point in time is to our research. If Wj is constant over j, we get the standard log-rank test statistic.
Neither the log-rank test nor the weighted log-rank test are usually calculated by hand; the arithmetic is too extensive.
3. Stratified Log-Rank Test
Stratified log-rank test: used when you want to control for a factor like age, sex, weight or some other variable. For example, you might have two groups and control for gender (men, women) giving four possible groups, or strata.
The log rank test allows us to find the relative survival distribution for two samples, but in its original form it doesn’t allow us to adjust for any special factors which might affect that. The stratified log rank test is the test you’d use when analyzing the survival distribution of two samples which are divided into two or more groups or “strata” based on common criteria that affect the outcome.
Stratified Log Rank Test Usage
Suppose you wanted to find the relative survival distribution of two groups of people with smallpox; one group takes a new drug and one takes a placebo. The log rank test would give you a statistic describing this. But your samples are not uniform; they can be divided into male and female segments. Adjusting for this in your analysis may give you more information.
Using a stratified log rank test might become important if either men or women were particularly susceptible to dying of smallpox, and the placebo and trial group did not contain an exactly equal number of male and female participants. So gender would be what we call a confounder. It’s a variable that is associated with every member of the data set, and it’s also causally related to the outcome of interest (survival).
It’s not necessarily binary; for instance, in a study on diabetes patients, one might want to stratify based on weight. Weight is causally related to survival, and you can divide your samples into however many discrete groups is convenient to your study.
Prerequisites and Assumptions of the Stratified Log Rank Test
Before using the stratified log rank test you’ll want to check that your variable of interest is not a confounding variable. It is only a confounder if it is actually in the causal pathway from the exposure (i.e. the independent variable) to the outcome (i.e. the dependent variable).
Using the stratified log rank test also assumes that the effect (survival) is similar across both strata of the confounder.
Running the Stratified Log Rank Test
To run the stratified log rank test:
- Calculate the log rank test statistic over each individual strata.
- Take the weighted mean of those individual log rank test statistics.
Let Us be the stratified log rank test statistic and Ui are the individual log rank test statistics over the set of j strata . Then you can write this as:
References:
Stanford University. Log-Rank Test. Retrieved September 3, 2017 from: https://web.stanford.edu/~lutian/coursepdf/unitweek3.pdf
Improved Logrank-Type Tests for Survival Data Using Adaptive Weights
The Log Rank Test. Retrieved September 3, 2017 from: http://myweb.uiowa.edu/pbreheny/7210/f15/notes/9-17.pdf
Log Rank Test in Neuroscience. Retrieved 9/4/2017 from: http://www.sciencedirect.com/topics/neuroscience/logrank-test
Log Rank Test. Retrieved 9/4/2017 from: https://web.stanford.edu/~lutian/coursepdf/unitweek3.pdf