What is a Weighted Mean?
A weighted mean is a kind of average. Instead of each data point contributing equally to the final mean, some data points contribute more “weight” than others. If all the weights are equal, then the weighted mean equals the arithmetic mean (the regular “average” you’re used to). Weighted means are very common in statistics, especially when studying populations.
Watch this video showing how to find a weighted mean:
The Arithmetic Mean.
When you find the “usual” mean for a set of numbers, all the numbers carry an equal weight. For example, if you want to find the arithmetic mean of 1, 3, 5, 7, and 10:
- Add up your data points: 1 + 3 + 5 + 7 + 10 = 26.
- Divide by the number of items in the set: 26 / 5 = 5.2.
What do we mean by “equal weight”? The first sentence in some tests (like this one) is sometimes “All questions carry an equal weight”). It’s saying that all the questions in the exam are worth the same number of points. If you have a 100 point exam and 10 questions, each question is worth 1/10th of the points. In the above question, you have of a set of five numbers. You can think of each number contributing 1/5 to the total mean (as there are 5 numbers in the set).
The Weighted Mean.
In some cases, you might want a number to have more weight. In that case, you’ll want to find the weighted mean. To find the weighted mean:
- Multiply the numbers in your data set by the weights.
- Add the results up.
For that set of number above with equal weights (1/5 for each number), the math to find the weighted mean would be:
1(*1/5) + 3(*1/5) + 5(*1/5) + 7(*1/5) + 10(*1/5) = 5.2.
Example problem: You take three 100-point exams in your statistics class and score 80, 80 and 95. The last exam is much easier than the first two, so your professor has given it less weight. The weights for the three exams are:
- Exam 1: 40 % of your grade. (Note: 40% as a decimal is .4.)
- Exam 2: 40 % of your grade.
- Exam 3: 20 % of your grade.
What is your final weighted average for the class?
- Multiply the numbers in your data set by the weights:
.4(80) = 32
.4(80) = 32
.2(95) = 19 - Add the numbers up. 32 + 32 + 19 = 83.
The percent weight given to each exam is called a weighting factor.
Need help with a homework question? Check out our tutoring page!
Weighted Mean Formula
The weighted mean is relatively easy to find. But in some cases the weights might not add up to 1. In those cases, you’ll need to use the weighted mean formula. The only difference between the formula and the steps above is that you divide by the sum of all the weights.
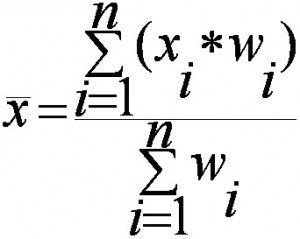
The image above is the technical formula for the weighted mean. In simple terms, the formula can be written as:
Weighted mean = Σwx/Σw
- Σ = summation (in other words…add them up!).
- w = the weights.
- x = the value.
To use the formula:
- Multiply the numbers in your data set by the weights.
- Add the numbers in Step 1 up. Set this number aside for a moment.
- Add up all of the weights.
- Divide the numbers you found in Step 2 by the number you found in Step 3.
In the example grades problem above, all of the weights add up to 1 (.4 + .4 + .2) so you would divide your answer (83) by 1:
83 / 1 = 83.
However, let’s say your weighted means added up to 1.2 instead of 1. You’d divide 83 by 1.2 to get:
83 / 1.2 = 69.17.
Warning: The weighted mean can be easily influenced by outliers in your data. If you have very high or very low values in your data set, the weighted mean may not be a good statistic to rely on.
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.