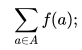Statistics Definitions > Weighting Factor
Contents:
1. Weight and the Weighting Factor.
A statistical weight is an amount given to increase or decrease the importance of an item. Weights are commonly given for tests and exams in class. For example, a final exam might count for double the points (double the “weight”) of an in-class test.
A weighting factor is a weight given to a data point to assign it a lighter, or heavier, importance in a group. It is usually used for calculating a weighted mean, to give less (or more) importance to group members. It is also used in statistical sampling for adjusting samples and in nuclear medicine for calculating effective doses.
2. Use In Sampling
Weighting factors are used in sampling to make samples match the population. For example, let’s say you took a sample of the population and had 41% female and 59% male. You know from census data that females should make up 51% of the population and males 49%. In order to make sure that you have a representative sample, you could add a little more “weight” to data from females. To calculate how much weight you need, divide the known population percentage by the percent in the sample. For this example:
- Known population females (51) / Sample Females (41) = 51/41 = 1.24.
- Known population males (49) / Sample males (59) = 49/59 = .83.
3. Use In Nuclear Medicine
Weighting factors are used extensively in radiologic and nuclear medicine to calculative effective doses for procedures. The calculations for Tissue Weighting Factors (sometimes called Radiologic Weighting Factors) account for the fact that different parts of the body absorb radiation at different rates.
A tissue weighting factor(WT) is assigned to body parts, with more radiosensitive parts given higher weighting factors.
Effective dose = individual organ dose values * WT.
Tissue weighting factors (ICRP) are:
- WT = 0.12: stomach, colon, lung, red bone marrow, breast, remainder tissues,
- WT = 0.08: gonads,
- WT = 0.04: urinary bladder, oesophagus, liver, thyroid,
- WT = 0.01: bone surface, skin, brain, salivary glands.
4. Weighting Factor and the Weight Function?
You may want to read this first: What is a Function?
A weight function is a special function that allows you to allocate more “weight” or influence to some elements of a set. Weight functions are often used on measured data, and can be used for both discrete variables and continuous variables.
The special weight function w(a): = 1 represents the unweighted situation where every element has the same weight.
Discrete Weight Function
Let’s say you are summing up a set of values; the values of a particular function f on A. Then we could write the sum as:
If we want to weight our values with the weight function w:A→ R+, the sum would be:
Reasons to Use Weighting Functions
There are a number of reasons you might choose to use weighting functions. If you are using a variety of measurement tools and you know that part of your data set is more accurate than another part, using weight functions can help you improve fit when you estimate unknown parameters or choose a curve to represent a model.
You might also weight to compensate for bias (errors). If we know that a number of data points are more biased than others, it makes sense to give them lower weights when determining your model.
Sometimes, a weight function doesn’t have anything to do with measurement errors or lack of accuracy due to bias. In engineering applications, weighting functions are used to reflect the relative influence of different forces or parameters. For instance, a force acting from a far distance would need lower weighting than a force acting from close proximity. Of course, weight functions can also be used when we are working with the actual force exerted by different weights on an object.
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
NIST Engineering Statistics Handbook. 4.4.5.2. Accounting for Non-Constant Variation Across the Data. Retrieved from https://www.itl.nist.gov/div898/handbook/pmd/section4/pmd452.htm on July 13, 2019.
NIST Engineering Statistics Handbook. 4.6.3.4 Weighting to Improve Fit. Retrieved from https://www.itl.nist.gov/div898/handbook/pmd/section6/pmd634.htm on July 13, 2019.