- What are “Odds”?
- What is the Odds Ratio?
- How to Calculate the Odds Ratio
- What do the Results mean?
- Population Averaged vs. Subject Specific Odds Ratio
Watch the video for an overview of the odds ratio and a couple of examples of calculations, or read on below:
What are “Odds”?
Odds Definition
Odds is usually defined in statistics as the probability an event will occur divided by the probability that it will not occur [1]. In other words, it’s a ratio of successes (or wins) to losses (or failures). As an example, if a racehorse runs 100 races and wins 20 times, the odds of the horse winning a race is 20/80 = 1/4.
The above odds definition is the odds in favor of an event. But there is another way to define odds in statistics— odds against an event happening. This is defined as the number of ways an event does not happen against the number of ways an event does happen [2]. For our racehorse example, that would be 80 to 20, or 4 to 1.
Odds vs. Probability
The odds definition is very similar to the definition of probability, which is the fraction of times an event occurs in a certain number of trials. In the horse example, the probability of a win is 20/100.
When there are a very small number of events, odds and probability are very similar. For example, let’s say the horse runs 4 races and wins 1. The odds of the horse winning a race is 1/3 (1 win to 3 losses) and the probability is 1/4 (1 win out of 4 races).
One major differences between odds and probability is that while odds range from 0 and infinity, probability ranges from 0 to 1.
Dictionary Definition of Odds
The statistical definition of odds is quite precise compared to dictionary definitions, which are inconsistent and have different meanings, even in a plain language sense instead of a statistical one [2]:
- “the chances of something happening” (Macmillan British Dictionary, 2012)
- “the probability that one thing is so or will happen rather than another; the ratio of the probability of one event to that of an alternative event” (Merriam-Webster Dictionary, 2012)
- “the ratio of the probability of an event’s occurring to the probability of its not occurring; the likelihood of the occurrence of one thing rather than the occurrence of another thing, as in a contest” (American Heritage Dictionary, 2012)
What is the Odds Ratio?
An odds ratio (OR) is a measure of association between a certain property A and a second property B in a population. Specifically, it tells you how the presence or absence of property A has an effect on the presence or absence of property B. The OR is also used to figure out if a particular exposure (like eating processed meat) is a risk factor for a particular outcome (such as colon cancer), and to compare the various risk factors for that outcome. You could use the OR to find out how much alcohol use leads to liver disease. Or you might want to find out if cell phone use has some link to brain cancer. As long as you have two properties you think are linked, you can calculate the odds.
How to Calculate the Odds Ratio
You have two choices for the formula:
(a/c) / (b/d)
or, equivalently:
(a*d) / (b*c)
General Steps:
Step 1: Calculate the odds that a member of the population has property “A”. Assume the person already has “B.”
Step 2: Calculate the odds that a member of the population has property “A”. Assume the person does not have “B.”
Step 3: Divide step 1 by step 2 to get the odds ratio (OR).
Odds Ratio Example
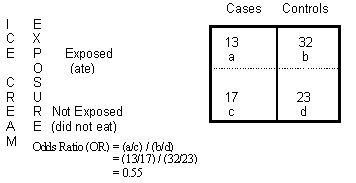
The above image shows two levels of exposure to ice cream: those who ate it, and those who didn’t. The 2×2 table also shows two outcome levels: people who were ill (“cases”) and people who were not (“controls”). The odds ratio is calculated as follows:
- Ill people: people who ate ice cream / people who did not = 13/17
- People who are not ill: people who ate ice cream / people who did not = 32/23
- Dividing the two results, we get (13/17) / (32/23) = 0.55
The resulting odds ratio of .55 means that ill people were about half as likely to eat ice cream as well people.
Odds Ratio Interpretation; What do the Results mean?
- An odds ratio of exactly 1 means that exposure to property A does not affect the odds of property B.
- An odds ratio of more than 1 means that there is a higher odds of property B happening with exposure to property A.
- An odds ratio is less than 1 is associated with lower odds.
However, it’s not quite as simple as that. You could think of the odds ratio as being a bit overly simplistic at describing real world situations. If, for example, you have a positive OR, it doesn’t mean that you have a statistically significant result. In order to figure that out, you need to consider the confidence interval and p-values (if you know it). The other issue is that even if you determine your results are statistically significant, that significance might not apply to all members of a population — there are nearly always a multitude of factors associated with risk. For example, this article points out that while overall, depression is strongly linked to suicide, “…in a particular sample, with a particular size and composition, and iBn the presence of other variables, the association may not be significant.”
Population Averaged vs. Subject Specific Odds Ratio
Population averaged models compare marginal distributions and give an overview of the effect on a whole population. The margins of a contingency table contain the totals, so it makes sense for them to be used to calculate the marginal odds ratio for a whole population. On the other hand, subject-specific models look at joint distributions: specific conditions or experiences within the model. The joint distributions are used to calculate conditional odds ratios.
Marginal Odds Ratio Example (for Population Averaged Models)
Michael Radelet studied death sentence data from Florida from 1976-77.* Calculate the marginal odds ratio for the race of defendant and whether or not that made a difference about if they got the death penalty:
| Defendant Race | Victim Race | Death Penalty Y | Death Penalty N |
| W | W | 19 | 132 |
| W | B | 0 | 9 |
| B | W | 11 | 52 |
| B | B | 6 | 97 |
Solution:
- Sum (marginalize) the values in the table. We’re interested in only the race of the defendant and whether or not they got the death penalty. Therefore, we can marginalize (sum up) values for the race of the victim. This creates a new 2×2 table:
Defendant Race Death Y Death N W 19 141 B 17 149 - Use the information in the marginal table to find the OR (using the OR formula from above):
OR = (a/c) / (b/d) = (19/17)/(141/149) = 1.12/0.95 = 1.18.
The odds are 1.18 times higher that a white defendant will get the death penalty compared to a black defendant.
*If you’re interested in his findings, he concluded that there isn’t any clear evidence to support the hypothesis that the defendant’s race is strongly associated with imposition of the death penalty. However, defendants were more likely to be sentenced to death if they had a white victim.
Subject specific models calculate the odds ratio using the same formula as all of the examples above. The only difference is that instead of summing all the variables together, you’ll hold one variable constant (i.e. you’ll use joint distributions).
Next: Adjusted Odds Ratio
References
[1] The Difference Between “Probability” and “Odds”. Retrieved November 26, 2021 from: https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/BS704_Confidence_Intervals10.html
[2] Fulton, L. et al. Confusion Between Odds and Probability, a Pandemic?
Journal of Statistics Education, Volume 20, Number 3 (2012) 3
www.amstat.org/publications/jse/v20n3/fulton.pdf
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Radelet, M. L. Racial Characteristics and the Imposition of the Death Penalty. American Sociological Review, v46 n6 p918-27 Dec 1981
Levine, D. (2014). Even You Can Learn Statistics and Analytics: An Easy to Understand Guide to Statistics and Analytics 3rd Edition. Pearson FT Press