Fubini’s theorem is a way to calculate a double integral using (usually, the much easier) iterated integrals; it allows the order of integration for iterated integrals to be changed.
Fubini’s theorem allows us to calculate a double integral over a rectangle. If a continuous function f(x, y) on a rectangle R = [a, b] x [c, d], then the double integral ∫∫ f(x, y)dA equals the iterated integral
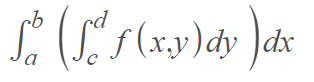
or, in a different order:
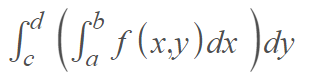
The inner integral in both cases can be evaluated with the fundamental theorem of calculus. The other variable is treated as a constant [1].
Fubini’s Theorem: Example
Example question: Evaluate the following double integral using Fubini’s theorem:
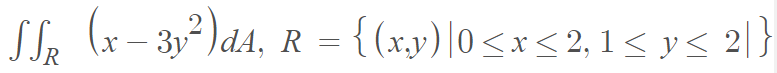
Solution: Integrating with respect to y:
Step 1: Set up the iterated integral:
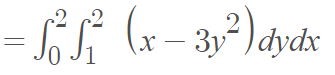
Step 2: Evaluate the “inside” integral:
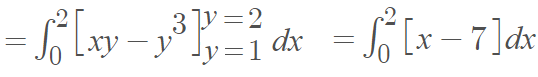
Step 3: Integrate with respect to x:
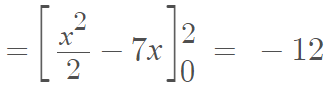
The solution (-12) can also be obtained by the re-ordered integral, according to the theorem. In other words, if you integrate with respect to x first, you’ll get the same answer:
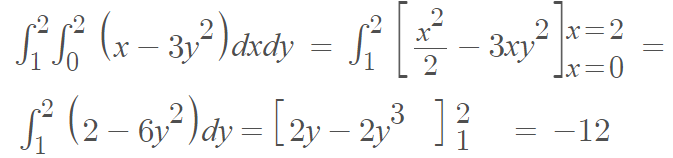
For this example, we could choose to integrate with respect to x first, or y first. Sometimes though, you’ll come across an ugly integral, perhaps requiring integration by parts or another “ugly” technique. You’ll usually want to choose whichever variable is easier to integrate. That said, a word of warning: Fubini’s theorem only works if the function is integrable over R. The theorem won’t work if you have a discontinuity, making it non-Integrable [2]. Sometimes you might not spot the discontinuity, especially if you’re integrating a complicated looking rational function.
However, the clue that there is something wrong (i.e., a discontinuity within the bounds of integration) will come when you integrate with respect to both variables: you will get different solutions. Therefore, if you aren’t a hundred percent sure that your function is integrable over R, it may be a good idea to check your solution by integrating twice (once with respect to x and once with respect to y).
Tonelli’s theorem is almost the same theorem (and in fact is also sometimes called “Fubini’s theorem”), except it applies to a non-negative measurable function rather than a function that is integrable over its domain.
References
[1] Fubini’s Theorem. Retrieved November 29, 2021 from: https://web.ma.utexas.edu/users/m408m/Display15-2-3.shtml
[2] A Fubini Counterexample. Retrieved November 29, 2021 from: https://math.jhu.edu/~jmb/note/nofub.pdf