What is a Tail Bound?
The tails of a random variable X are those parts of the probability mass function far from the mean [1].
Sometimes we want to create tail bounds (or tail inequalities) on the PMF, or bound the probability that the random variable deviates a long way from the mean. For example, if the PMF represents a budget, we might not want to go over that budget by a factor of 3. Or, if I expect 10,000 people with student loans are in default, I might want to know the probability a million borrowers will default.
Types of Tail Bound
Various formulas exist for tail bounds. One way to place a tail bound is by controlling the moments of the random variable X.
Markov’s inequality is the simplest tail bound, only requiring the existence of the first moment. It states that, for a nonnegative random variable X with mean μ = εX [2],
Pr(X ≥ k) ≤ μ/k.
Although simple, the bounds that Markov’s inequality implies are usually not useful because they are too weak.
The Chebyshev bound is slightly stronger than Markov’s inequality. It is defined for a random variable X with mean μ = εX with standard deviation σ = √(ε((X – μ)2)) for any δ ≥ 1:
Pr(|X – μ ≥ δσ) ≤ δ-2.
Gaussian Tail Bound via Chernoff
One of the more complex tail bounds is the Chernoff bound, which requires that the moment generating function exists. For many random variables, this requirement is usually not a problem because the MGF will exist in a neighborhood around 0 [3]. The Chernoff bound can be used to find a Gaussian tail bound and has several equivalent forms. One form is for Poisson trials Xi with sum X = ΣiXi and mean μ = εX, for any δ > 0:
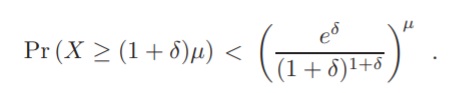
References
PMF Image: Qwfp, <https://creativecommons.org/licenses/by-sa/3.0>CC BY-SA 3.0 , via Wikimedia Commons
[1] Tail bounds. Retrieved November 28, 2021 from: https://courses.cs.washington.edu/courses/cse312/11au/slides/09tails.pdf
[2] Supplementary Lecture I: Tail Bounds. Retrieved November 28, 2021 from: http://www.cs.cornell.edu/courses/cs681/2007fa/Handouts/tailBounds.pdf
[3] Intermediate Statistics Fall 2019. Retrieved march 9, 2023 from http://www.stat.cmu.edu/~siva/705/lec2.pdf