Fundamental Theorem of Calculus
The fundamental theorem of calculus explains how to find definite integrals of functions that have indefinite integrals. It bridges the concept of an antiderivative with the area problem.
Contents:
Fundamental Theorem of Calculus Part One
The formula for the first fundamental theorem is:
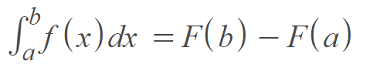
The formula is saying that the definite integral from a to b for a function f(x) is equal to the integral function evaluated at b, minus the integral function evaluated at a.
The last part of the above can be written as a more compact notation, which means the same thing as F(b) – F(a) [1]:
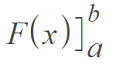
When you figure out definite integrals (which you can think of as a limit of Riemann sums), you might be aware of the fact that the definite integral is just the area under the curve between two points (upper and lower integral bounds. You are finding an antiderivative at the upper and lower limits of integration and taking the difference. The Fundamental Theorem of Calculus justifies this procedure.
Fundamental Theorem of Calculus Example
Example problem: Evaluate the following integral using the fundamental theorem of calculus:
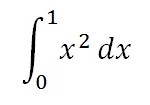
Step 1: Evaluate the integral. This particular integral is evaluated using the integral rule for power functions:
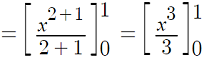
Note: For an indefinite integral, you would normally include the + C; Here we’re ignoring it, as we want to find a specific area.
Step 2: Find the value of the integral at b, which is the value at the top of the integral sign in the problem. In this example, the upper bound of the integral, b is 1, so:
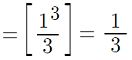
Step 3: Find the value of the integral at a, which is the value at the bottom of the integral sign in the problem. In this example, the value of “a” is 0, so:
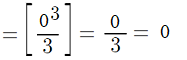
Step 4: Subtract a (Step 3) from b (Step 2):
⅓ – 1 = ⅓
That’s it!
Back to top
Second Fundamental Theorem of Calculus
The second fundamental theorem builds off of the first and formally establishes a relationship between a function and its antiderivative.
If f is a continuous function on an open interval containing point a, then every x in the interval can be described by:
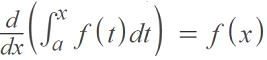
In English: First, integrate the function, then differentiate it. You’ll end up with the original function. In other words, it shows the symbiotic relationship:
- F(x) is the antiderivative of f(x) and
- f(x) is the derivative of F(x).
In order for the second fundamental theorem of calculus to work, a must be a constant and x must be a variable.
The second fundamental theorem gives us a powerful way to find calculate definite integrals:
- Find the antiderivative,
- Evaluate the antiderivative at the integral bounds.
The second fundamental sounds the same as the first and the two are very similar. In fact, they do have the same content [2]. However, they are worded slightly differently. The first theorem was really just telling us to subtract F(b) – F(a). The second theorem is telling that if we have a constant c as the lower bound of integration, a continuous function has a unique antiderivative A that satisfies A(c) = 0.
Example: Second FTC
Example question: Calculate the following:

Solution: Plugging our function into the second fundamental theorem, we get:
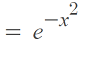
References
[1] Larson, R. & Edwards, B. (2016). Calculus. Cengage Learning.
[2] MIT: Chapter 14. The Second Fundamental Theorem of Calculus. Retrieved April 25, 2021 from: http://www-math.mit.edu/~djk/18_01/chapter14/contents.html