Fresnel integrals are a class of functions known for their application to understanding light diffraction patterns through an aperture and their unique ability to generate the famous “Cornu Spiral.” First, we will define the Fresnel integral as a set of parametric equations. Then, we will perform a power series expansion—a common technique for evaluating the integral of a transcendental function. Finally, we’ll look towards the application of Fresnel integrals in the worlds of mathematics and physical science.
Defining the Fresnel Integral
Fresnel integrals are a pair of functions that take the form:
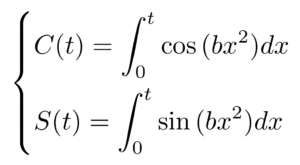
Where b are real-valued constants.
Equations written this way are known as parametric equations, meaning that the equations’ values are related by an independent variable. In the case above, t represents the parameter that the two functions share.
Unfortunately, this formulation of the Fresnel integral is often not desirable. This is because the integral must be evaluated (or approximated) for a given value of t before the function output can be known. Next, we’ll explore an alternate way to write the Fresnel integrals that avoids this problem.
Rewriting the Fresnel Integral: Power Series Method
We can rewrite the Fresnel integrals above by leveraging a math trick called power series expansion. In a power series expansion, we replace a trigonometric function or otherwise transcendental function with a polynomial that has infinite terms. Each function has a unique series of terms that correspond to its power series expansion.
We will begin by treating the function C(t).
Step 1: Replace the cosine function with its unique infinite sum of terms as written below.
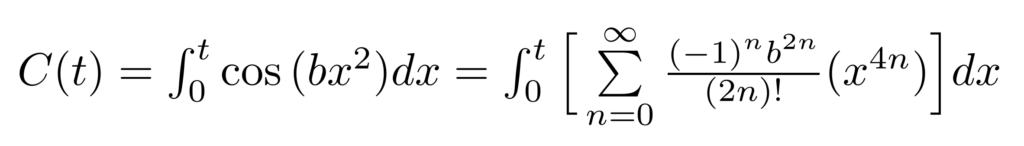
Step 2: Move the integral symbol inside of the sum. We can do that because the integral of a sum is the sum of its integrals. Then, we can use the power rule to evaluate the definite integral.
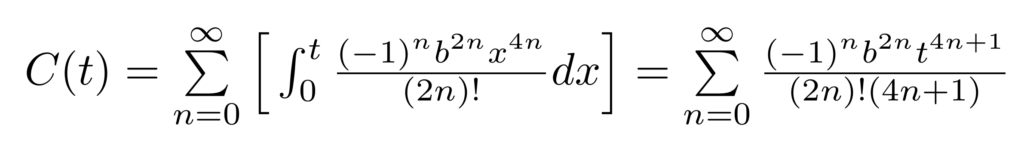
Above, notice that the function C(t) has now been re-written without the integral—our original goal behind the power series expansion technique! With this new formulation of the Fresnel integral, we can approximate the value of C(t) for a given parameter value by considering the first several terms in the summation.
We can repeat this process for the second function, S(t). The only difference in our approach will be to choose a different power series expansion.
Step 1: Replace the sine function with its unique infinite sum of terms as written below.
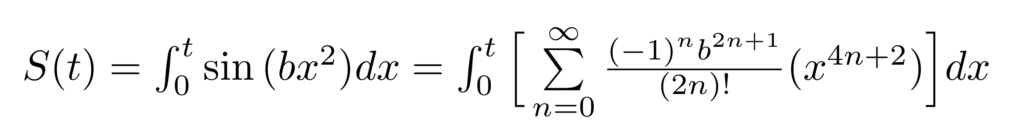
Step 2: Like before, move the integral inside of the summation and evaluate it using the power rule.
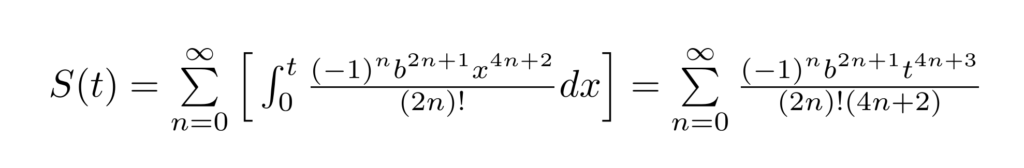
It really is that quick! In fact, the power series expansion technique is good to remember because it can be applied to many integrals involving transcendental functions.
Visualizing the Fresnel Integral
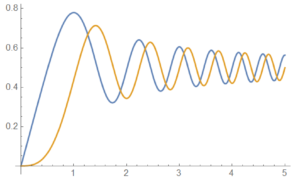
The graph below represents the value of the Fresnel integral for a range of t values at a value of b = 1. C(t) is shown in blue, while S(t) is shown in orange. The two functions correlate in their movement, but they are slightly offset from each other. This effect can be attributed to the 90-degree difference between sine and cosine.
If the two functions are considered together, then a unique pattern emerges. Below, C(t) and S(t) are plotted together in the plane of the page, while t can vary. The ‘swirly’ structure that results is known as a Cornu Spiral, shown below.
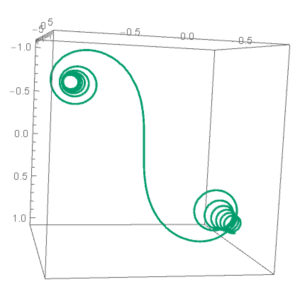
At t = 0, the Cornu Spiral sits at the origin. As t approaches infinity, the Cornu Spiral approaches (0.5,0.5). Similarly, the Cornu Spiral approaches (-0.5, -0.5) as t tends towards negative infinity.
Applications to Physics
In addition to generating the miraculous Cornu Spiral, the Fresnel integral can be used to solve the diffraction pattern of a light source through a close aperture. This is a consequence of the fact that circle waves are of the form
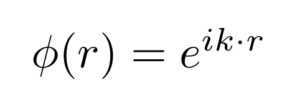
Applying Euler’s formula, which states that an exponential of this form can be restated as a combination of sine and cosine functions, is how we arrive at the original parametric equation. The expression for light intensity can then be written as
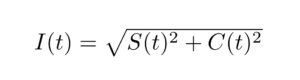
References
Mielenz, Klaus. “Computation of Fresnel Integrals.” Journal of Research of the National Institute of Standards and Technology. Vol. 102, No. 3, May–June 1997. Accessed May 24, 2020. https://pdfs.semanticscholar.org/1ce9/3369e4cd8e1b321ce1276b819bcbb298b404.pdf
S. Albeverio and S. Mazzucchi, “Generalized Fresnel integrals.” Bulletin des Sciences Mathématiques. Vol. 129, No. 1, 2005, pp. 1-23. Accessed May 24, 2020. http://www.sciencedirect.com/science/article/pii/S0007449704000776