Hypothesis Testing > Decision rule
This article is about the decision rule used in Hypothesis Testing. For the decision rule used in clinical trials, see: Adaptive Design Clinical Trials.
A decision rule spells out the circumstances under which you would reject the null hypothesis. The null hypothesis is the backup ‘default hypothesis’, typically the commonly accepted idea which your research is aimed at disproving. In general, it is the idea that there is no statistical significance behind your data or no relationship between your variables.
Usually a decision rule will usually list specific values of a test statistic, values which support the alternate hypothesis (the hypothesis you wish to prove or test) and which are contradictory to the null hypothesis.
Test Statistics and the Decision Rule
How the decision rule is used depends on what type of test statistic is used: whether you choose to use an upper-tailed or lower-tailed (also called a right-tailed or left-tailed test) or two-tailed test in your statistical analysis.
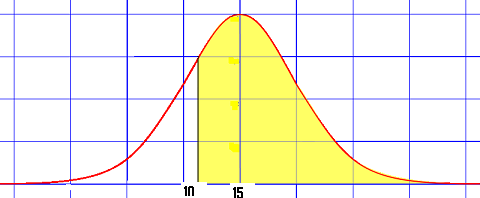
If you’re using an upper-tailed test, your decision rule would state that the null hypothesis will be rejected if the test statistic is larger than a (stated) critical value. For a lower-tailed test, the rule would state that the hypothesis should be rejected if the test statistic is smaller than a given critical value.
In the case of a two-tailed test, the decision rule would specify rejection of the null hypothesis in the case of any extreme values of the test statistic: either values higher than an upper critical bound or lower than another, lower critical bound.
The set of values for which you’d reject the null hypothesis is called the rejection region. It’s bounded by the critical value given in the decision rule.
Next: Admissible Decision Rule
References
LaMorte, W. (2017). Hypothesis Testing: Upper, Lower, and Two- Tailed Tests Retrieved from http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_HypothesisTest-Means-Proportions/BS704_HypothesisTest-Means-Proportions3.html on February 18, 2018
Zou, Jingyu. AMS 102 Lecture Notes: Decision Rule and How to Form Them
Retrieved from http://www.ams.sunysb.edu/~jasonzou/ams102/notes/notes3.pdf on February 18, 2018