Statistics Definitions > Curvilinear Regression
Contents:
Curvilinear Definition
Curvilinear lines are smooth lines or curves, like the curves we see in trigonometric functions or parabolic functions. “Curvilinear” refers to something more complicated though, than just a simple curve or set of curves—it’s a set of curves with a purpose.
For example, during curvilinear regression, the procedure considers an infinite number of curves—or at the least, a very large family of curves. That leads us to a slightly more formal (and general) definition: In general, we can say that something is curvilinear if it is formed (or characterized by) a set of curved lines. That doesn’t mean you need to have a large number of lines: a single curved line still counts as a set of one.
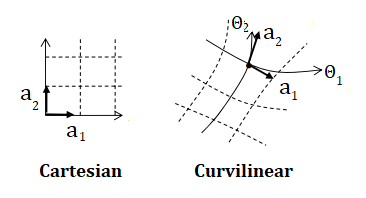
Curvilinear Coordinates
Curvilinear coordinates are a coordinate system used for Euclidean space where the coordinate lines (think: the x and y-axis, and the grid lines on your graph paper) may be curved. You can think of curvilinear coordinates as a generalized coordinate system, free of the straight line restraints that you see with a Euclidean system.
Curvilinear coordinates don’t have to be based on curved lines. Cartesian coordinates are one type of curvilinear coordinate systems. But so are cylindrical coordinates (an extension of two-dimensional polar coordinates to three-dimensional) and spherical polar coordinates. If there’s a one to one mapping between coordinate systems, we can convert between them. For example, the mapping between spherical polar coordinates and Cartesian coordinates uses these equivalences:
![]()
Different systems are given different names, depending on how they intersect:
- If the intersections are right angles, the system is called an orthogonal coordinate system.
- Otherwise, it is a skew coordinate system.
The image below shows three coordinate systems in two dimensional space, as well as the mappings between them.
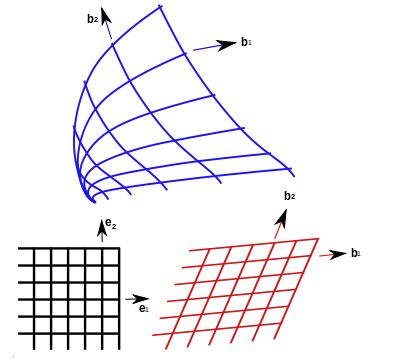
Why use Curviliear Coordinates?
If you wanted to map a roller coaster, a spherical cell, or the shape of a biological cell, the usual lines in a x-y plane won’t quite do. However, if you have an infinite number of curves to play with, then you would be able to create a more accurate representation of just about every real-life system. These representations can help you to see aspects of the problem that might not be readily apparent in a regular Cartesian plane.
However, a Cartesian coordinate system is usually easier to work with.
Curvilinear Regression
Curvilinear regression involves finding the equation of a curved line that fits a particular set of data points. You might use this type of regression if you’ve begun analyzing a data set with linear regression, and then you realize that the correlation between your x and y variables doesn’t really look like a straight line— it looks more like a curve.
Polynomial regression (which includes quadratic regression and cubic regression) is a frequently used method of curvilinear regression. What type of curve you decide to fit your data to should depend on a preliminary study of the data. You will want to use the simplest possible curve that fits the data well.
References
Antoni, M. (2018). Calculus with Curvilinear Coordinates: Problems and Solutions. Springer.
1.16 Curvilinear Coordinates. Retrieved September 12, 2019 from: http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_1_Vectors_Tensors/Vectors_Tensors_16_Curvilinear_Coordinates.pdf
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. Pages 213-219. Retrieved online from http://www.biostathandbook.com/curvilinearregression.html on June 22, 2019.
Curvilinear Regression
Coordinates
Although Cartesian coordinate planes are drilled into us in school, the reality is very few real life events or data sets fit that neatly right-angled system. Coordinate systems are curvilinear if they are made from intersecting, curved surfaces. 
The mathematics behind these beautiful coordinate systems are beyond the scope of this statistics site. However, you can find what I consider to be a clear description (mathematically speaking) of the system on James Foadi’s site.
Reference:
Foadi, J. 2005. Gradient, Divergence and Curl. Available online here.