Hierarchical Cluster Analysis > Complete linkage clustering
Complete linkage clustering (farthest neighbor ) is one way to calculate distance between clusters in hierarchical clustering. The method is based on maximum distance; the similarity of any two clusters is the similarity of their most dissimilar pair.
Complete Linkage Clustering vs. Single Linkage
Complete linkage clustering is the distance between the most distant elements in each cluster. By comparison, single linkage measures similarity of the most similar pair.
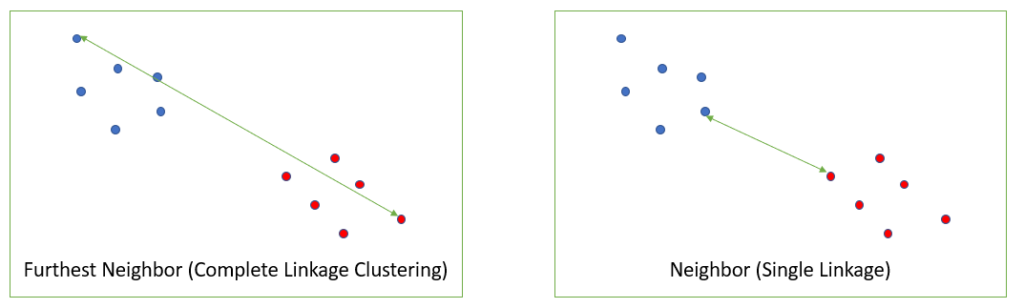
Which one you use (single linkage or complete linkage) depends on your data and what you want to achieve by clustering. Single linkage can result in long stringy clusters and “chaining” while complete linkage tends to make highly compact clusters [1].
One disadvantage of complete linkage clustering is that it behaves badly when outliers are present [2]. This is not a problem with single linkage.
Example of Complete Linkage Clustering
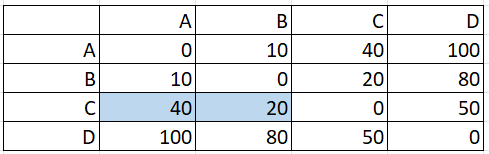
The following distance matrix shows pairwise distances between elements A, B, C, and D:
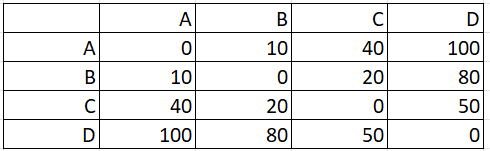
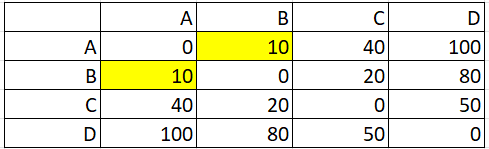
Step 1: Identify the pair with the shortest distance. For this example, that’s A, B.
Step 2: Make a new matrix with the combined pair (from Step 1). At this stage, we know the diagonal will be all zeros (because the distance between any point and itself is zero):
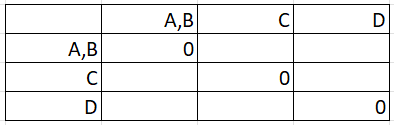
The matrix is reflected across the diagonal, so we only need to find values for the lower half (below the row of zeros).
Step 3: Fill in the first blank entry by finding the maximum distance. The first blank entry is at the intersection of C and A,B:
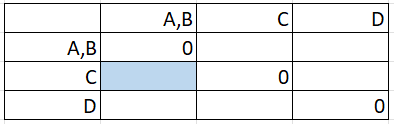
Looking in the matrix from Step 1, the distance C to A is 40 and C to B is 20:
The maximum of these two distances (40 & 20) is 40, so that gets placed in the cell:
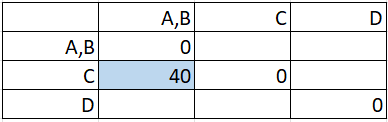
Step 4: Fill in the remaining boxes, finding the maximum distance between pairs, repeating the technique in Step 3:
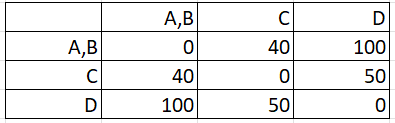
Step 5: Repeat Steps 2 to 4 on the new matrix you created in Step 4 above. In other words, your Step 4 matrix becomes your new Step 1 matrix. If you find the max distances for these new pairs, you should end up with:
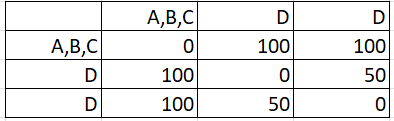
Continue until all items have been clustered. For this example, you have to work through the steps one more time to get:
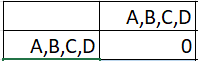
References
[1] Adams, R. Hierarchical Clustering. Article posted on Princeton.edu. Retrieved November 22, 2021 from: https://www.cs.princeton.edu/courses/archive/fall18/cos324/files/hierarchical-clustering.pdf
[2] Milligan, G. W. (1980). An examination of the effect of six types of error perturbation on fifteen clustering algorithms. Psychometrika, 45, 325–342