General Term: Definition, Examples

Sequence and Series >

The general term (sometimes called the nth term) is a formula that defines a sequence.

For example, for the sequence defined by a_n = 1/n, the first four terms are found by plugging in 1, 2, 3, 4 for “n”:
1/1, 1/2, 1/3 and 1/4.
Different sequences have different formulas.

The general term is one way to define a sequence. The other way is the recursive definition of a sequence, which defines terms by way of other terms. For example, A_n = A_n-1 + 4.

General Term for Arithmetic Sequences

The general term for an arithmetic sequence is a_n = a₁ + (n – 1) d, where d is the common difference.

Example question: What is the general term of the sequence 2, 5, 8,…?
Solution:

1. Find d by subtracting the second from first term: d = 5 – 2 = 3.
2. Plug d into the general formula: a_n = a₁ + (n – 1) 3
3. Plug in the first term for a₁: a_n = 2 + (n – 1) 3

The general term is a_n = 2 + (n – 1) 3

General Term for Geometric Sequences

For a geometric sequence, the formula is a_n = a₁ r^{n – 1}, where r is the common ratio.

Example question: What is the general term of the geometric sequence 8, 4, 2,…?
Solution:

1. Find r the ratio of any two consecutive terms. I’ll use the second and third terms in this example: r = 2/4 = ½.
2. Plug r into the general formula: a_n = a₁ ½^{n – 1}
3. Plug in the first term for a₁: a_n = 8 (½)^{n – 1}

The general term is a_n = 8 (½)^{n – 1.}

Using Algebra

If you don’t know what kind of sequence you have, you may have to use a little logic and your knowledge of algebra to get your terms into a workable form. For example, let’s say you’re asked to find the general term for the sequence


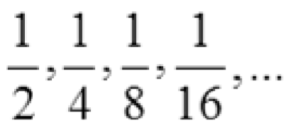
This becomes much easier to work with if you change the denominators into exponents (giving an exponential sequence):


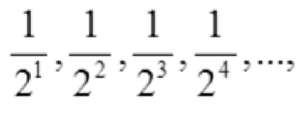
Which gives a_n = ½ⁿ

References

Steig, J. 1999. Sequences & Series – General terms. Retrieved January 20, 2021 from: http://www.mesacc.edu/~marfv02121/readings/seq_def/