Skewness > Bowley Skewness
What is Bowley Skewness?
 Bowley skewness is a way to figure out if you have a positively-skewed or negatively skewed distribution. One of the most popular ways to find skewness is the Pearson Mode Skewness formula. However, in order to use it you must know the mean, mode (or median) and standard deviation for your data. Sometimes you might not have that information; Instead you might have information about your quartiles. If that’s the case, you can use Bowley Skewness as an alternative to find out more about the asymmetry of your distribution. It’s very useful if you have extreme data values (outliers)or if you have an open-ended distribution.
Bowley skewness is a way to figure out if you have a positively-skewed or negatively skewed distribution. One of the most popular ways to find skewness is the Pearson Mode Skewness formula. However, in order to use it you must know the mean, mode (or median) and standard deviation for your data. Sometimes you might not have that information; Instead you might have information about your quartiles. If that’s the case, you can use Bowley Skewness as an alternative to find out more about the asymmetry of your distribution. It’s very useful if you have extreme data values (outliers)or if you have an open-ended distribution.
Bowley Skewness Formula.
Watch the video for an overview:
Bowley Skewness = (Q3+Q1 – 2Q2) / (Q3 – Q1)
- Skewness = 0 means that the curve is symmetrical.
- Skewness > 0 means the curve is positively skewed.
- Skewness < 0 means the curve is negatively skewed.
Bowley Skewness Worked Example
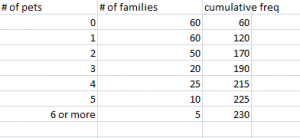
Q. Find the Bowley Skewness for the following set of data:
Step 1: Find the Quartiles for the data set. You’ll want to look for the “nth” observation using the following formulas:
Q1 = (total cum freq + 1 / 4)th observation = (230 + 1 / 4 ) = 57.75
Q2 = (total cum freq + 1 / 2)th observation = (230 + 1 / 2 ) = 115.5
Q3 = 3 (total cum freq + 1 / 4)th observation = 3(230 + 1 / 4) = 173.25
Step 2: Look in your table to find the nth observations you calculated in Step 1:
Q1 = 57.75th observation = 0
Q2 = 115.5th observation = 1
Q3 = 173.25th observation = 3
Step 3: Plug the above values into the formula:
Skq = (Q3 + Q1 – 2Q2) / (Q3 – Q1)
Skq = (3 + 0 – 2) / (3 – 0) = 1/3
Skq = + 1/3, so the distribution is positively skewed.
Why Bowley Skewness works.
In a symmetric distribution, like the normal distribution, the first (Q1) and third (Q3) quartiles are at equal distances from the mean (Q2). In other words, (Q3-Q2) and (Q2-Q1) will be equal. If you have a skewed distribution then there will be a difference between those two values.
Limitations of Bowley Skewness.
Bowley Skewness is an absolute measure of skewness. In other words, it’s going to give you a result in the units that your distribution is in. That’s compared to the Pearson Mode Skewness, which gives you results in a dimensionless unit — the standard deviation. This means that you cannot compare the skewness of different distributions with different units using Bowley Skewness.
Alternative Bowley Skewness formula.
According to Business Statistics, Bowley recognized that the Bowley Skewness formula could not be used to compare different distributions with different units. For example, you can’t compare a distribution measured in heights in cm with one of weights in pounds. He offered an alternative formula. You should use this formula if you want to compare different distributions with different units:
Relative Skewness = ((Q3 + Q1) – (2 * Median ))/ (Q3 – Q1).