A bounded interval (or finite interval) has real numbers for both endpoints. Sequences are bounded if contained within a bounded interval [1].
- Examples of bounded intervals:
- [0, 1]: Includes both endpoints, 0 and 1,
- [99, 1999]: Includes endpoints 99 and 1999.
- Examples of unbounded intervals:
- (-∞, ∞): does not have a real number for either endpoint,
- The set of all real numbers (ℝ).
- Examples of half-bounded intervals:
- (-∞ 1]
- The set of natural numbers(ℕ) [2].
Bounded and unbounded intervals can also be closed or open intervals. Open intervals have parentheses and do not include endpoints. Closed intervals, which have brackets, include endpoints. The difference between closed and bounded is that bounded intervals have to have real numbers, while closed intervals can have other numbers, like complex numbers.
Theorems that Work on a Bounded Interval
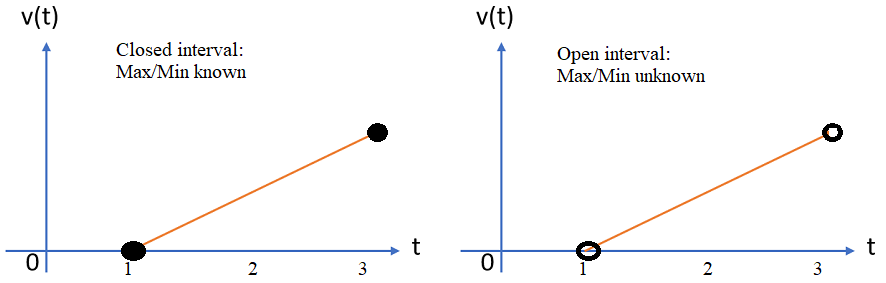
Whether or not intervals are bounded rarely crops up as a topic in elementary calculus classes. However, many theorems and procedures only work on these carefully defined intervals. Even if it isn’t explicitly stated in class, working with bounded intervals is implied. For example, all of the following theorems and procedures are defined on bounded intervals:
- All continuous functions are Riemann integrable.
- If a function is continuous on an interval [a, b], then it has an absolute maximum and an absolute minimum on that same interval [3].
- The mean value theorem (for derivatives) states that a continuous function has at least one point where the function is equal to its average value on an interval.
- The mean value theorem (for integrals) states that there is a rectangle equal to the area under the curve on an interval.
There are dozens more theorems that only work on a bounded interval.
References
[1] Math 401 – Introduction to Real Analysis. Retrieved April 25, 2021 from: http://personal.psu.edu/axb62/PSPDF/lnotes401.pdf
[2] Additional Topics from 4.2 and 4.3. https://www.math.tamu.edu/~jlewis/131notes/131notes4.2,4.3.pdf
[3] Part 1: The Real Numbers. Retrieved April 25, 2021 from: https://www.math.uh.edu/~charles/Real-nos.pdf