Within-Group Variation: Definition and Examples

ANOVA > Within-Group Variation

What is Within-Group Variation?

Within-group variation (sometimes called error group or error variance) is a term used in ANOVA tests. It refers to variations caused by differences within individual groups (or levels). In other words, not all the values within each group (e.g. means) are the same. These are differences not caused by the independent variable.

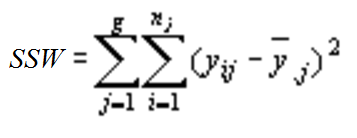
Each sample is looked at on its own. In other words, no interactions between samples are considered. For example, let’s say you had four groups, representing drugs A B C D, with each group composed of 20 people in each group and you’re measuring people’s cholesterol levels. For within-group variation, you’ll look at variances in cholesterol levels for people in group A, without considering groups B,C, and D. Then you would look at cholesterol levels for people in group B, without considering groups A,C, and D. And so on.

ANOVA Output

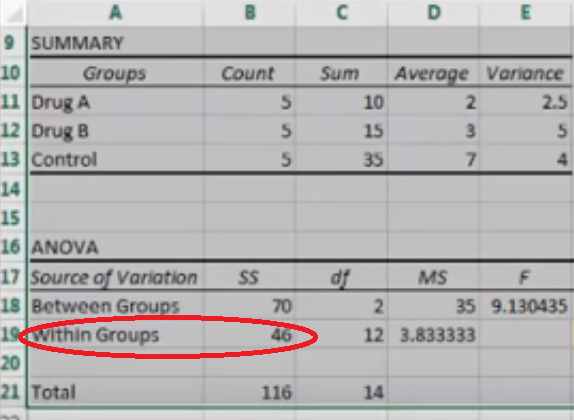
Within-group variation is reported in ANOVA output as SS(W) or which means Sum of Squares Within groups or SSW: Sum of Squares Within. It is intrinsically linked to between group variation (Sum of Squares between), variance difference caused by how groups interact with each other. This is because the whole point of ANOVA is to compare the ratio of within group variance and between group variance. In fact, the core of the ANOVA test — the F statistic — is calculated by dividing the between group variance by the within group variance.

If the variance caused by interactions between different samples is much greater than the variance found inside values in a single group, that indicates the means aren’t equal.

Degrees of freedom for Within-group variaton equals the sum of the individual degrees of freedom for each sample in the test.

References

Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.