The significance level or alpha level is the probability of making the wrong decision when the null hypothesis is true. Alpha levels (sometimes just called “significance levels”) are used in hypothesis tests. Usually, these tests are run with an alpha level of .05 (5%), but other levels commonly used are .01 and .10.
Watch the video for an overview:
Contents (click to go to that section):
- Type I and II errors
- How do I Calculate an Alpha Level for one- and two-tailed tests?
- Why is an Alpha Level of .05 commonly used?
1. Alpha Levels / Significance Levels: Type I and Type II errors
In hypothesis tests, two errors are possible, Type I and Type II errors.
Type I error: Supporting the alternate hypothesis when the null hypothesis is true.
Type II error: Not supporting the alternate hypothesis when the alternate hypothesis is true.
In an example of a courtroom, let’s say that the null hypothesis is that a man is innocent and the alternate hypothesis is that he is guilty. if you convict an innocent man (Type I error), you support the alternate hypothesis (that he is guilty). A type II error would be letting a guilty man go free.
An alpha level is the probability of a type I error, or you reject the null hypothesis when it is true. A related term, beta, is the opposite; the probability of rejecting the alternate hypothesis when it is true.
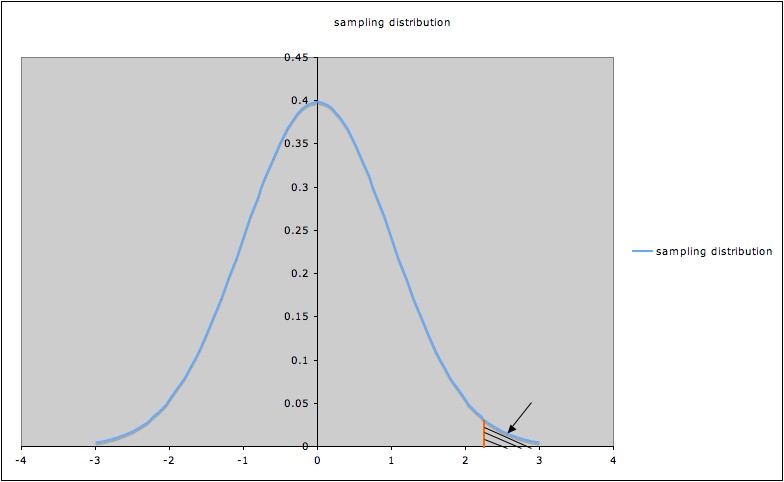
This graph shows the rejection region to the far right.
2. How do I Calculate an Alpha Level for one- and two-tailed tests?
Watch the video for an overview:
Need help with a specific homework question? Check out our tutoring page!
Alpha levels can be controlled by you and are related to confidence levels. To get α subtract your confidence level from 1. For example, if you want to be 95 percent confident that your analysis is correct, the alpha level would be 1 – .95 = 5 percent, assuming you had a one tailed test. For two-tailed tests, divide the alpha level by 2. In this example, the two tailed alpha would be .05/2 = 2.5 percent. See: One-tailed test or two? for the difference between a one-tailed test and a two-tailed test.
3. Why is an alpha level of .05 commonly used?
Seeing as the alpha level is the probability of making a Type I error, it seems to make sense that we make this area as tiny as possible. For example, if we set the alpha level at 10% then there is large chance that we might incorrectly reject the null hypothesis, while an alpha level of 1% would make the area tiny. So why not use a tiny area instead of the standard 5%?
The smaller the alpha level, the smaller the area where you would reject the null hypothesis. So if you have a tiny area, there’s more of a chance that you will NOT reject the null, when in fact you should. This is a Type II error.
In other words, the more you try and avoid a Type I error, the more likely a Type II error could creep in. Scientists have found that an alpha level of 5% is a good balance between these two issues.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Picture courtesy of the University of Texas.