Modified Thompson Tau Test

Outliers > Modified Thompson Tau Test

What is the modified Thompson Tau Test?

The modified Thompson Tau test is a way to find outliers in a data set. The data set must be a single variable (e.g. x1, x2,…xn). One potential outlier is tested at a time using a version of the t-test. Roughly speaking, the Tau test eliminates outliers more than two standard deviations away from the mean.

Like most tests for outliers, there is the possibility that you could eliminate good data (especially if there is a cluster of outliers), so you should interpret the results of the test with caution.

Running the Test

In order to run the test, you first have to identify a possible outlier.

Example question: Are any of the following points outliers? : 489, 490, 490, 491, 494, 499, 499, 500, 501, and 505.

Part 1: Identify a potential outlier

Step 1: Find the sample mean. The mean for this set of data is 495.8.

Step 2: Subtract the mean from the highest and lowest data point to find the absolute value of the differences. As a formula, that’s:
δi = |xi – x̄|.
So:

  • |489 – 495.8.| = 6.8
  • |505 – 495.8.| = 9.2

The point with the highest absolute difference (δ) is a suspected outlier. This is the one you’ll test. For this example, that’s 9.2.

Part 2: Test the data point

Step 1: Look up the sample size (n) in the Tau table below to get the Tau value (for the formula behind the table calculations see Tau Formula below):
For a sample size of 10, Tau is 1.7984.

Step 2: Calculate the standard deviation (s) for the sample. For this set of data, s = 5.67.

Step 3: Multiply Tau (Step 1) by s (Step 2):
Tau * s = 1.7984 * 5.67 = 10.2

Step 4: Compare the absolute difference (δ) for the suspected outlier (from Part 1) with Tau * s (Step 3).
If δ > Tau * s, the point is an outlier.
9.2 is not greater than 10.2, so is therefore not an outlier.

Repeating the Steps

In the above example, the point with the largest absolute difference was not an outlier. If the point is an outlier, repeat the steps above for the point with the next largest deviation. However, when you repeat the calculations, you must remove the outlier you identified before recalculating the mean and finding the new Tau.

Tau Table

n Tau n Tau n Tau
3 1.1511 21 1.8891 40 1.9240
4 1.4250 22 1.8926 42 1.9257
5 1.5712 23 1.8957 44 1.9273
6 1.6563 24 1.8985 46 1.9288
7 1.7110 25 1.9011 48 1.9301
8 1.7491 26 1.9035 50 1.9314
9 1.7770 27 1.9057 55 1.9340
10 1.7984 28 1.9078 60 1.9362
11 1.8153 29 1.9096 65 1.9381
12 1.8290 30 1.9114 70 1.9397
13 1.8403 31 1.9130 80 1.9423
14 1.8498 32 1.9146 90 1.9443
15 1.8579 33 1.9160 100 1.9459
16 1.8649 34 1.9174 200 1.9530
17 1.8710 35 1.9186 500 1.9572
18 1.8764 36 1.9198 1000 1.9586
19 1.8811 37 1.9209 5000 1.9597
20 1.8853 38 1.9220 → ∞ 1.9600

Tau Formula


If you’re using the table, you don’t really need the formula (unless you’re calculating some specific sample size not listed). Tau is calculated from T critical values of student’s T-distribution, which identify a rejection region. The formula is:
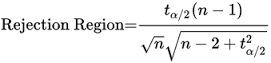
Tau Formula

Where:


Comments? Need to post a correction? Please Contact Us.