Partial Correlation & Semi-Partial: Definition & Example

Correlation Coefficients >

Contents:

1. Partial Correlation
2. Semi-Partial Correlation

What is Partial Correlation?

Partial correlation measures the strength of a relationship between two variables, while controlling for the effect of one or more other variables. For example, you might want to see if there is a correlation between amount of food eaten and blood pressure, while controlling for weight or amount of exercise. It’s possible to control for multiple variables (called control variables or covariates). However, more than one or two is usually not recommended because the more control variables, the less reliable your test.

Partial correlation has one continuous independent variable (the x-value) and one continuous dependent variable (the y-value); This is the same as in regular correlation analysis. In the blood pressure example above, the independent variable is “amount of food eaten” and the dependent variable is “blood pressure”. The control variables — weight and amount of exercise — should also be continuous.

Notation

A period in the subscript separates the correlated variables and the controlled for variables. For example, correlating caloric intake (X₁) against blood pressure (X₂), while controlling for weight (X₃), is written as:
r_12.3
Alternatively, a bar is used instead of a period and subscript: r(1,2|3).

Running the Test

The correlation coefficient, r, is also used to show the results from partial correlation. Like the regular correlation coefficient, r_partial returns a value from -1 to 1.

Partial correlation is usually carried out by running multiple regression analysis. Some software programs include partial correlation. For example, in SPSS choose Analyze > Correlations > Partial.

How to Interpret the Result

If the partial correlation, r_12.3, is smaller than the simple (two-variable) correlation r₁₂, but greater than 0, then variable 3 partly explains the correlation between X and Y.

Semi-Partial Correlation

Semi-partial correlation is almost the same as partial. In fact, many authors use the two terms to mean the same thing. However, others do make the following subtle distinction:

With semi-partial correlation, the third variable holds constant for either X or Y but not both; with partial, the third variable holds constant for both X and Y.

For example, the semi partial correlation statistic can tell us the particular part of variance, that a particular independent variable explains. It explains how one specific independent variable affects the dependent variable, while other variables are controlled for to prevent them getting in the way.

To find it, calculate the correlation between the dependent variable and the residual of the prediction of one independent variable by the others.

Example

Suppose we use a set of data (from a 2002 paper from Abdi et al.) which lists three variables over six children. Each child was tested for memory span (Y) and speech rate (X₂), and their age was also noted. A correlation statistic was desired which predicts Y (memory span) from X₁ and X₂ (age and speech rate).

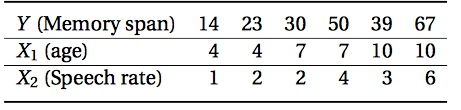
Normally, in a situation where X₁ and X₂ were independent random variables, we’d find out how important each variable was by computing a squared coefficient of correlation between X₁ and X₂ and the dependent variable Y. We would know that these squared coefficients of correlation were equal to the square multiple coefficient of correlation. But in a case like ours, X₁ and X₂ are anything but independent. Speech rate is highly dependent on age, and so using the squared coefficient will count the contributions of each variable several times over.

References

1. Abdi, Herve. Part (Semi Partial) and Partial Regression Coefficients. Retrieved from https://www.utdallas.edu/~herve/Abdi-PartialRegressionCoefficient2007-pretty.pdf on May 8, 2018
2. Abdi, H., Dowling, W.J., Valentin, D., Edelman, B., & Posamentier M. (2002). Experimental Design and research methods. Unpublished manuscript. Richardson: The University of Texas at Dallas, Program in Cognition.
3. Brannick, M. Partial and Semipartial Correlation. Retrieved from http://faculty.cas.usf.edu/mbrannick/regression/Partial.html on May 8, 2018
4. Sharpa, J. (2007). Business Stats. Pearson Education India.
5. STATISTICA Help. Semi-Partial (or Part) Correlation. Retrieved from http://documentation.statsoft.com/STATISTICAHelp.aspx?path=glossary/GlossaryTwo/S/SemiPartialorPartCorrelation on May 8, 2018
6. Weatherburn, C. (1949). A First Course Mathematical Stats. CUP Archive.