- What is Velocity?
- The Velocity Function
- Finding velocity with calculus
- Average Velocity
- Velocity of a Falling Object:
- Speed (Calculus)
- Projectile Motion
See also: Instantaneous Velocity
Watch the video for three examples or read on below:
What is Velocity?
![By MichaelMaggs [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons velocity of a falling object](https://www.statisticshowto.com/wp-content/uploads/2018/09/velocity-1-97x300.png)
As calculus is the mathematical study of rates of change, and velocity is the measure of the change in position of an object with respect to time, the two come in contact often. Finding the velocity of basic functions can be done without the use of calculus. However, when the graph of a function is curved the change isn’t constant, and performing calculus operations becomes necessary.
The Velocity Function
This gives you an object’s rate of change of position with respect to a reference frame (for example, an origin or starting point), and is a function of time. It tells the speed of an object and the direction (e.g. 70 km/h south). It is usually denoted as v(t). For example, v(t) = 2x2 + 9.
Note that this is different from the velocity equation you probably came across in algebra. The equation v = S/T gives you the average velocity of an object, given distance and time. The function enables you to find instantaneous change as well as average change. It must also meet the requirements for being a function.
Sign
The sign of the function tells you the direction the object is traveling.
- Positive: v(t) > 0 = motion to the right on the number line (i.e. in a positive direction).
- Negative: v(t) < 0 = motion to the left on the number line (i.e. in a negative direction).
If an object is traveling in a straight line (i.e. with rectiliear motion), you can use the sign to tell you whether the object is speeding up or slowing down:
- Slowing down: velocity and acceleration have opposite signs (e.g. + -).
- Speeding up: they have the same sign (e.g. + +).
Watch the video for an example of to use the function to find total distance traveled.
How to Find The Velocity Function
You can use differentiation and integration to find the function. The following image shows the relationship between the first few derivatives and integrals as they relate to the velocity function:
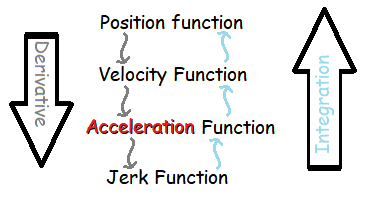
The derivative of the position function gives you the velocity of a moving object, assuming the object is a/ moving in a straight line and b/ air resistance is zero. More formally, we say that the velocity of an object is the rate of change of an object’s position, with respect to time.
As an example, let’s say you were given a position function. You can differentiate it (i.e. take the first derivative) to get the velocity function. For an example of how to do this, see: Velocity of a Falling Object.
On the other hand, if you have a jerk function you’re going to want to work backwards. In other words, you need to integrate the function. How you do this depends on what type of function you have. See: Integral Rules.
Finding Velocity
How you solve for a falling object depends upon what information you’ve been given. For example, if you’ve been given a time (usually in seconds), then the velocity of any falling object can be found with the equation v = g * t, where g is acceleration due to gravity. However, if you’ve been given a position function (e.g. for the height), then you need a little calculus to derive the answer.
If you are given the position function (for the distance moved by the object), you can take the derivative and reach the function. If you are given the formula for the object’s acceleration, you can find the integral and again come to the solution.
1. Given a Position (Displacement) Function
Example question: Find the velocity function for the following position function:x(t) = 4t2 + 4t + 4
Step 1: In order to get from the displacement to the velocity, you will take the derivative of the displacement with respect to time. First, set up your equation to get ready to find a derivative:
x(t) = 4t2 + 4t + 4
dx/dt = d/dt 4t2 + 4t + 4 = v(t)
Step 2: Solve for the derivative. Here you can use the Power Rule, and rule for derivative of constants.
d/dt 4t2 + 4t + 4 = 8t + 4
v(t) = 8t + 4
That’s it!
Tip: The velocity is not constant over time, so t makes an appearance. If it were constant, it would not have the variable in it, and it would also have an acceleration of 0.
2. Find velocity function given Acceleration.
Example question: Find the velocity function from the following acceleration function:
a(t) = 10t + 5
Step 1: Set up the equation to perform an integration:
a(t) = 10t + 5
v(t) = ∫ a(t) dt = ∫ 10t + 5 dt
Step 2: Perform integration on a(t). Integration is a somewhat advanced calculus method, so be sure to take a look at the articles specifically detailing it (see: Integrals) if you are unfamiliar with it.
∫ a(t) dt = ∫ 10t + 5 dt = 5t2 + 5t + c = v(t)
Note: c is a constant of integration that can’t be determined without more information. If you are supplied an initial value, you can find the constant by setting time equal to 0. Using the above for example:
v(0)= 5(02) + 5(0) + c = c = v(0)
Average Velocity
Average velocity is defined in terms of the relationship between the distance traveled and the time that it takes to travel that distance. The formula for finding average velocity is:
vav = xf – xi / tf – ti
Where:
- vav is the average velocity,
- xf is the final position of the object,
- xi is the initial position of the object,
- tf is the final time,
- ti is the initial time.
Example:
 A car starts at position x = 16 feet. After 8 seconds the car is 134 feet east of its initial position. What is the car’s average velocity?
A car starts at position x = 16 feet. After 8 seconds the car is 134 feet east of its initial position. What is the car’s average velocity?
Step One: Find the difference between the initial and final positions of the car.
The car traveled from 16 feet to 134 feet (134 – 16 = 118). The car traveled east a total of 118 feet.
Step Two: Calculate the amount of elapsed time, if it isn’t explicitly stated. We know that the car traveled for 8 seconds. No further calculations are required here.
Step Three: Plug the values into the formula and solve.
Vav = 118ft / 8s = 14.75 ft/s east
The average velocity that the car traveled was 14.75 feet-per-second eastward.
1. Velocity of a Falling Object: v = g*t
A falling object is acted on by the force of gravity: -9.81 m/s2 (32 ft/s2). Gravity will accelerate a falling object, increasing its velocity by 9.81 m/s2 (or or 32 ft/s2) for every second it experiences free fall.
In order to find the velocity of a particular falling object, just multiply gravity (g) by time(t). The formula is:
v = g * t
v = -9.81 m/s2*t
Example #1: An object falls for 1.2 seconds. What is its velocity?
- v = -9.81 m/s2*t
- v = -9.81 m/s2*1.2s
- v = 11.77200 m/s
2. Velocity of a Falling Object Using Calculus
Calculus is very useful for finding the velocity of a falling object if all you have is a position function, like the height of an object. First, differentiate the position function to get the velocity function. Then use that function to find the answer.
Example #2: Position Function
The function v(t) is the derivative of the position function. If you’re given a position equation like h(t) or s(t), you’ll need to differentiate that function in order to find the velocity of the falling object.
Example problem: Frustrated with your calculus class, you attach a rocket to it and launch it down from your dorm window. The height of the book, in feet over the car after t seconds is given by the function h(t) = 200 – 16t2. The book will dent your car if it’s going more than 100 feet per second. Will your car get dented?
Hint:The given equation is not for the velocity of a falling object. It is a position function.
Step 1: Differentiate the position function, h(t) = 200 – 16t2 to get the function (you need to know the velocity to answer the question).
- 200 is a constant, so it disappears.
- 16t2 can be differentiated using the power rule.
The differentiated function is 2(16)t2-1 = -32t.
Step 2: Solve the position function for zero (in other words, when the height is zero) to find out when the book will hit the car.
Setting h(t) = 0 gives:
- 0 = 200 – 16t2
- t = 14.14213…
Step 3: Insert your answer from Step 2 into the function from Step 1:
- v(14.14213) = -32(14.14213)
- v(14.14213) = -452.54816
The velocity is -452.54816 feet per second when the book hits the car. This is more than 100 feet per second. Yes, there will be a dent!
That’s it!
Tip: A negative sign indicates the height is decreasing.
Other Useful Equations
If you are given the height/distance the object has fallen (d), then use this equation to find the time (t):
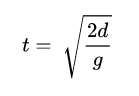
If you are given the height/distance the object has fallen (d), then use this equation to find the instantaneous velocity of the object:
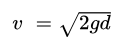
If you are given the height/distance the object has fallen (d), then use this equation to find the average velocity of the object:
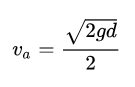
What is Speed?

Speed (Common Usage)
In everyday language, “speed” tells you how quickly an object travels between two places.
The formula is as follows:
S = D/T
- S = Speed
- D = Distance
- T = Time
S, D, and T can have different units. For example:
- S = miles-per-hour (mph) or kilometers-per-hour.
- D = miles, millimeters or feet.
- T = larger intervals like light years or smaller ones like nanoseconds.
Sometimes “velocity” and “speed” are used to mean the same thing. However, there are very important distinctions between the two when used in calculus (or physics).
Speed: Calculus Definition
Speed takes on a more precise definition when used in calculus. It is defined as the absolute value of velocity:
S = │v(t)│
Where:
- t = time
Speed is a scalar quantity represented by magnitude (i.e. an amount) and doesn’t have a direction—unlike velocity, which is a vector with both magnitude and direction. Speed measures the rate of motion regardless of direction, and is measured in distance per units of time. As you’re taking the absolute values, it is always positive.
Example: Calculating Speed using Derivatives
We don’t really calculate “speed” in calculus, so if you’re asked a question like “how fast is the object traveling”, what the question is really asking you for is the velocity of the object.
When you’re given a position function, you find velocity with the position function’s first derivative:
s′(t) = v(t)
Example question: Based on the function of s(t) = t3 + 4t feet at time (t), find S at t = 4.24 seconds.
Step 1: Take the derivative of the function s(t) = t3 + 4t:
- s′(t) = v(t)
- v(t) = 3t2 + 4
Step 2: Plug the given time (in this example, that’s t = 4.24 seconds) into the function you found in Step 1:
- v(4.24) = 3(4.24)2 + 4
- v(4.24) = 3(17.9776) + 4
- v(4.24) = 53.93 + 4
- v(4.24) = 57.93
Step 3: Find the absolute value:
- S = │v(4.24)│ = 4.24 seconds = 57.93 feet/second
The object is traveling at 57.93 feet per second at 4.24 seconds.
Projectile Motion
Projectile motion is the motion of an object which has no force acting on it but the gravitational field. This type of object is called a projectile.
Watch this video for an excellent overview of what a projectile motion is (with the NFL and Lester Holt):
Projectile Motion Without Initial Velocity
In the simplest kind of projectile motion problems, there is no initial velocity. An object is simply dropped so that the Earth’s magnetic field pulls it toward the ground at a rate of 9.81 m/s2.This acceleration is all in a vertical direction (i.e. toward the Earth’s surface). Gravity doesn’t have a horizontal component, and so (unlike the football in the above video), there isn’t any horizontal component to this type of acceleration: the object simply drops straight down.
For example, if you stuck your hand out of a skyscraper window and dropped an apple, it would have a velocity of 0 at the moment you opened your hand (t0). At t = 1 second, the apple would be traveling at 9.81 m/s2. At k seconds in, it would be traveling downward at a speed of 9.81m/s2k, supposing it hadn’t hit the ground yet and assuming (for simplicity) that we can ignore drag.
Projectile Motion With Initial Velocity
Many times, a projectile will begin with an initial velocity. We defined a projectile as an object which has no force acting on it in the present except the gravitational field. It’s important to realize, though, that it may have had other forces acting on it in the past. Your hand, for instance, may have been exerting force on the ball as you threw it out.
Suppose you are standing by the window in your building, 150 meters above the earth, and you throw your ball at an angle of 20 degrees above the horizontal, with an initial speed of 8.40 m/s.
The moment the ball leaves your hand, at t0, it is traveling at 8.40 m/s, and from that point forward the only force acting on it is gravity, which gives it an acceleration of 9.81 m/s2. The ball begins by going up, but one second later, it will already have begun moving down. You can’t add or subtract these rates directly; they are vector quantities, which means we have to pay attention to direction and add and subtract only what matches.
Let’s say that you are standing at the origin of a simple x y Cartesian coordinate system. When you throw that ball out at a 20 degree angle, its velocity will have two parts. Call them v0x and v0y. Draw a triangle, and use your geometry skills to solve for v0x and v0y.
- v0x = v0x cos (20) = 8.40 cos(20) = 7.893 m/s, and
- v0y = v0y sin (20) = 8.40 sin 20 = 2.873.
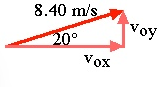
Since we’re pretending the effect of drag is negligible, there is no force acting on our ball horizontally: ax = 0. v0x = vx = 7.893 m/s at every point until the ball crashes to the ground.
It’s the vertical velocity that will be acted on by gravity. At t0 that was 2.873, in a + or upward direction, and gravity causes it to accelerate at 9.81 m/s2 in a – or downward direction. One minute in, it’s vertical speed will be 2.873 – 9.81 = -6.937, or about 6.9 m/s in a downward direction.
References
Allain, Rhett. Projectile Motion. Introductory Physics Lab. Retrieved from https://www2.southeastern.edu/Academics/Faculty/rallain/plab193/page1/page31/page31.html on January 26, 2019
Duffy, Andrew. Projectile Motion Example. Retrieved from http://physics.bu.edu/~duffy/semester1/c3_projectile.html on January 26, 2019
References
Bauer, W. & Westfall, G. (2011). University Physics. McGraw Hill.
Davis, D. (2002). Retrieved May 16, 2019 from: https://www.ux1.eiu.edu/~cfadd/1150/02-1DMtn/Speed.html
The Calculus of Motion.