How to Find a Coefficient of Variation: Contents:
What is the Coefficient of Variation?
The coefficient of variation (CV) is a measure of relative variability. It is the ratio of the standard deviation to the mean (average). For example, the expression “The standard deviation is 15% of the mean” is a CV.
The CV is particularly useful when you want to compare results from two different surveys or tests that have different measures or values. For example, if you are comparing the results from two tests that have different scoring mechanisms. If sample A has a CV of 12% and sample B has a CV of 25%, you would say that sample B has more variation, relative to its mean.
Formula
The formula for the coefficient of variation is:
Coefficient of Variation = (Standard Deviation / Mean) * 100.
In symbols: CV = (SD/x̄) * 100.
Multiplying the coefficient by 100 is an optional step to get a percentage, as opposed to a decimal.
Coefficient of Variation Example
A researcher is comparing two multiple-choice tests with different conditions. In the first test, a typical multiple-choice test is administered. In the second test, alternative choices (i.e. incorrect answers) are randomly assigned to test takers. The results from the two tests are:
| Regular Test | Randomized Answers | |
| Mean | 59.9 | 44.8 |
| SD | 10.2 | 12.7 |
Trying to compare the two test results is challenging. Comparing standard deviations doesn’t really work, because the means are also different. Calculation using the formula CV=(SD/Mean)*100 helps to make sense of the data:
| Regular Test | Randomized Answers | |
| Mean | 59.9 | 44.8 |
| SD | 10.2 | 12.7 |
| CV | 17.03 | 28.35 |
Looking at the standard deviations of 10.2 and 12.7, you might think that the tests have similar results. However, when you adjust for the difference in the means, the results have more significance:
Regular test: CV = 17.03
Randomized answers: CV = 28.35
The coefficient of variation can also be used to compare variability between different measures. For example, you can compare IQ scores to scores on the Woodcock-Johnson III Tests of Cognitive Abilities.
Note: The Coefficient of Variation should only be used to compare positive data on a ratio scale. The CV has little or no meaning for measurements on an interval scale. Examples of interval scales include temperatures in Celsius or Fahrenheit, while the Kelvin scale is a ratio scale that starts at zero and cannot, by definition, take on a negative value (0 degrees Kelvin is the absence of heat).
How to Find a Coefficient of Variation: Overview.
Need help with a specific homework question? Check out our tutoring page!
Use the following formula to calculate the CV by hand for a population or a sample.
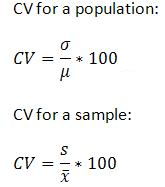
σ is the standard deviation for a population, which is the same as “s” for the sample.
μ is the mean for the population, which is the same as XBar in the sample.
In other words, to find the coefficient of variation, divide the standard deviation by the mean and multiply by 100.
How to find a coefficient of variation in Excel.
You can calculate the coefficient of variation in Excel using the formulas for standard deviation and mean. For a given column of data (i.e. A1:A10), you could enter: “=stdev(A1:A10)/average(A1:A10)) then multiply by 100.
How to Find a Coefficient of Variation by hand: Steps.
Example question: Two versions of a test are given to students. One test has pre-set answers and a second test has randomized answers. Find the coefficient of variation.
| Regular Test | Randomized Answers | |
| Mean | 50.1 | 45.8 |
| SD | 11.2 | 12.9 |
Step 1: Divide the standard deviation by the mean for the first sample:
11.2 / 50.1 = 0.22355
Step 2: Multiply Step 1 by 100:
0.22355 * 100 = 22.355%
Step 3: Divide the standard deviation by the mean for the second sample:
12.9 / 45.8 = 0.28166
Step 4: Multiply Step 3 by 100:
0.28166 * 100 = 28.266%
That’s it! Now you can compare the two results directly.
Check out our YouTube channel for more stats help and tips.