Torus: Definition, Examples

Calculus Definitions >

Torus: Definition

A Torus (plural: tori) is a geometric surface, generated by the revolution of a circle of radius R; The revolution occurs a distance r away from a center point.

The circle, which has no thickness, creates a tube with constant diameter and hollowness. The existence of the Torus is limited to a minimum dimension of the third dimension. Higher-dimensional tori are known as n-tor1 or hypertori.

Variations

Three forms of tori can be formed depending on the behavior of the axis of revolution.

1. If the axis of revolution does not have the revolved circle intersecting with itself, a normal torus is formed.
2. If the axis of revolution has the revolved circle intersect at a tangent point, the surface created becomes a horn torus. The horn is depicted as a spike on the inside.
3. If the axis of revolution passes the revolved circle twice, a spindle torus is formed. The insides of spindle tori contain an egg-like geometry.

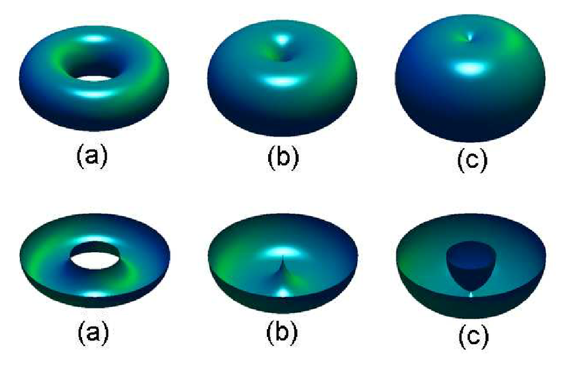
If the axis of revolution passes through the center of the revolved circle, a sphere would be generated instead of a torus.

Geometric Fundamentals

For all types of tori, there are parameters that are common through each that make it possible for their graphical depictions to exist. The radius from the center of the torus to the center of the revolving circle is the Major Radius, set as R. The radius of the circle itself is known as the Minor Radius, set as r.

Two angles exist (θ, φ) where θ represents the rotation angle the revolved circle takes (usually a full rotation is taken, aka 0 to 360 degrees). The φ angle is the tilt angle of the revolved circle such that a more complex bend can be made.

Toti can be graphed parametrically by the following equations (Ximera Team):

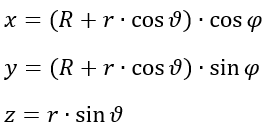
If the angles are unknown, tori can be graphed using implicit equations on the Cartesian Coordinate System.

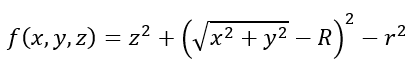
The parameters themselves, for both major and minor radii, can be found by moving terms around from the graphing function f(x, y, z) (Kriz, 2020).

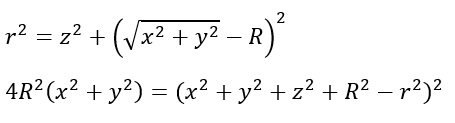
For the radii R and r, the relationships between them make the basis of the aspect ratio (the ratio of the size of the shape in different dimensions) and relate to the type:

• R > r; the revolved surface resembles regular tori.
• R = r; the revolved circles intersect with themselves at one tangent to form horn tori.
• R < r; the revolved surface self-intersects itself to form a spindle torus.

Torus Area and Volume Equations

If you visualize regular tori as encompassed cylinders, the area of is that for cylinders of radius r and height R:

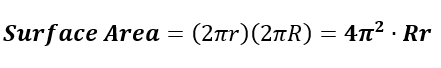
For a torus’ volume, the integral of the surface area with respect to the revolving circle’s radius r results in the following equation:

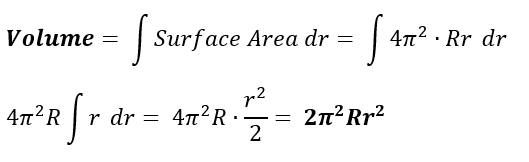
Real-World Applications

There are numerous man-made products that resemble the shape of tori. For example: doughnuts, O-rings, lifebuoys, and coffee cup handles. Although the hollow property doesn’t exist for these objects, the circular winding in each example assists in their specific scenarios. For example, lifebuoy flotation is made possible because its large surface area displaces more water weight than its own weight.

For applications in mathematics, a study can be done on the material stretch that occurs when forming a torus. A flat sheet can take the shape of a torus but distorts its surface to account for both the wrapping as a cylinder and the bending to connect the cylinder’s ends. Material tension can be studied by the formation of a torus to determine if the durability can handle such disfigurement when starting as a sheet.

Torus vs. Toroid

The two terms are often used synonymously, but there is a subtle difference.

The torus is produced by rotating a circle.
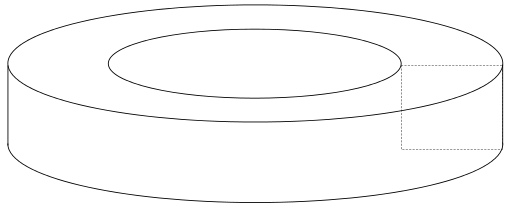
A toroid is a surface of revolution you get by rotating a closed curve around an axis. A toroid can be any geometric shape. For example, the following toroid shows a rotated square:

References

“Drawing a Torus.” Ximera, Ohio State University, ximera.osu.edu/mooculus/calculus3/normalVectors/digInDrawingATorus.

Kriz, Jiri. “Torus.” Nosco Mathematics, 2020, www.nosco.ch/mathematics/en/torus.php.