Unit Sphere: Definition
A unit sphere is a set of points that are distanced 1 unit away from a starting point (an “origin“).
The collection of points can exist in d-dimensions from one-dimensional to infinite-dimensional spaces. The collection of points is not required to look like a sphere to be considered unit spheres; only that their formation points are 1 unit away from the unit sphere’s center (Guruswami). An example is a polyhedron, that can take an infinite number of congruent faces.
Hyperspheres are a type of unit Sphere made up of a set of points 1 unit away from their center. The space they exist in is one dimension higher than their geometry.
For example, a circle existing in the third dimension is considered a hypersphere. Graphical visualization of hyperspheres is limited to the third dimension, but the properties of hyperspheres can still be mathematically examined.
Unit Sphere in Higher Dimensions
The unit hypersphere is a type of n-hypersphere (n-sphere)—a generalization of the circle and unit sphere to higher dimensions.
In n-terms, the 2D circle is a 2-hypersphere and the unit circle has a radius of 1. A 3D sphere is a 3-hypersphere and the unit sphere is a collection of points a distance of “1” from a fixed central point. The unit hypersphere is the next dimension up: a 4-hypersphere with a collection of points (x, y, u, v) so that x2 + y2 + u2 + v2 = 1. Add a fourth dimension to the unit sphere, and you get the unit hypersphere.
What Does an N-Sphere Look Like?
If you’re having trouble visualizing what a 4D sphere (or higher) looks like, you aren’t alone. Most people (with perhaps, the exception of Einstein), can’t perceive 4D naturally. This article by John D. Norton on four dimensional space does a great job at explaining how you can get from a one dimensional line to a four dimensional hypercube. As far as spheres, this is what a 4D sphere looks like (note how it collapses in on itself):

Foundation Formulas
For a third-dimensional sphere of radius one, the function that accounts for all points to satisfy such a geometry is:
f(x, y, z) = x 2 + y 2 + z 2 = 1
Unit spheres, within a Euclidean space of n dimensions, exists as a (n-1)-dimensional sphere with points that satisfy:
![]()
Where each xn represents a coordinate space that extends to n-dimensions. This equation follows suit to a third-dimensional sphere where an increase in dimensional space adds another squared dimension variable.
Area Formula
For a unit sphere and hypersphere, its formulas for area and volume depend upon what dimensional the geometry exists in. The area formula written as Sn starts its root at the integral of the Gaussian function closest to calculating the length of a one-dimensional sphere:
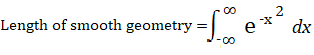
Where x currently has no meaning to any parameters of a sphere since the Gaussian Function acts as a building block to calculating surface areas of smooth geometries. A workable form of the volume equation for a three-dimensional sphere is:
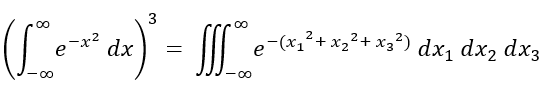
To which we can replace to Cartesian coordinates (x1, x2, x3) into spherical coordinates.
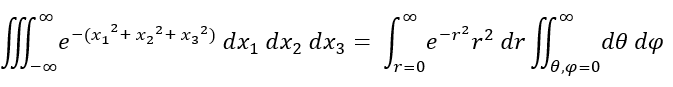
But what if we take the Gaussian Function Integral into higher dimensions? Letting the integral be raised to n-power results in:
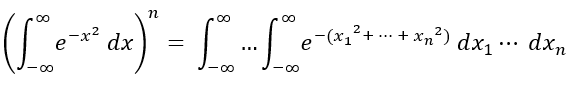 ]
]
Where the n-cartesian coordinates can be converted to coordinates known as Hyperspherical Coordinates. The following substitutions can be done to formulate the surface area formula in integral form:
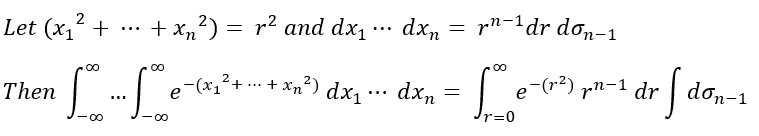
Where the angular integral containing dσn-1 represents the surface area of an n-sphere. We can denate that as Sn.
For the radial integral part that contains dr, we can multiply by a special “1” to rewrite the radial integral into a special function called the Gamma Function. For now, let the angular integral fall out from the procedure in achieving the Gamma Function as it will soon be seen to fall out on its own.
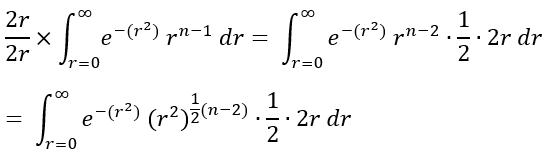
Performing u-substitution on the integral above takes the form of a Gamma Function:
Let u = r2 and du = 2r dr
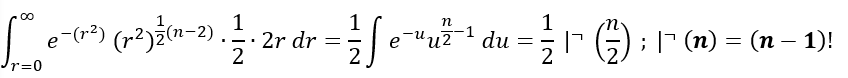
By combining the Gamma Function portion to the target surface area function gets to use a workable function to solve for Sn exactly as a function. We can equate the function below to the answer from the Gaussian Equation when we raise it by n:
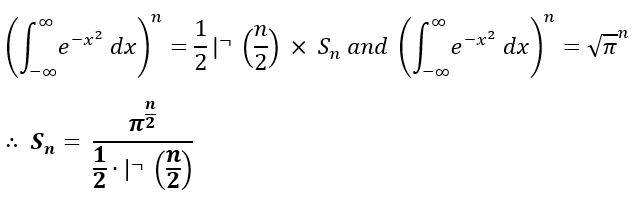
Volume Formula
Continuing off from the area formula and the idea that the change in the surface area represents the volume, Vn, of that same surface:
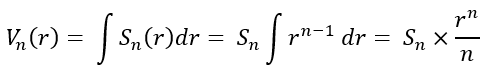
Whereby setting the radius value r = 1:
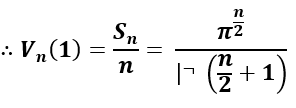
Volume/Area Observations
One may initially think that a Unit Sphere or Hypersphere taking place in n-dimensions takes up a lot of space. For both the area and volume equations, solving them manually for increasing n-values tells a different story.
The visual below can best show how the area and volume shift its growth initially to about n = 5 and then concaves downward towards zero (Glee, 2018).
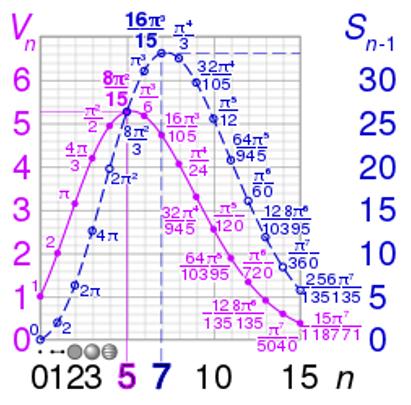
The behavior of the Gamma Function is responsible for this phenomenon since the Gamma Function grows towards infinity as the n-value gets larger. A larger denominator as the n-value increases forces both the area and volume rational functions to equal 1∞, which equals zero.
Unit Sphere: References
Banchoff, T. Coordinates for Circles and Spheres. Retrieved January 15, 2019 from: http://www.math.brown.edu/~banchoff/Beyond3d/chapter8/section09.html
Glee, C. M.. “Hypersphere Volume and Surface Area Graphs.” Accessed from Wiki Media, 20 Feb. 2018.
Guruswami , Vekatesan, and Ravi Kannan. “High-Dimensional Space.” Computer Science Theory for the Information Age, Carnegie Mellon University, www.cs.cmu.edu/~venkatg/teaching/CStheory-infoage/chap1-high-dim-space.pdf.Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.
Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 96-101, 1988.
Sommerville, D. M. Y. An Introduction to the Geometry of n Dimensions. New York: Dover, p. 136, 1958.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986