The Metropolis-Hastings algorithm is a popular statistical sampling method used in statistics and data science. It is a Markov chain Monte Carlo (MCMC) algorithm, meaning that it uses random samples from a probability distribution to estimate parameters. In this blog post, we will discuss what the Metropolis-Hastings algorithm is, how it works, and where it has been used.
What is the Metropolis-Hastings Algorithm?
The Metropolis algorithm is a random walk adaptation combined with acceptance-rejection sampling which converges on a specified target distribution (Gelman et al., 2013). One of the simplest types of MCMC algorithms, it was named for Metropolis et al. (1953) and Hastings (1970).
The algorithm is used in Bayesian Hypothesis testing to sample from posterior distributions, where direct sampling is difficult or impossible. It can approximate a posterior distribution (i.e. create a histogram) comprised of any combination of prior probabilities and sampling models. It can also be used for Monte Carlo integration to calculate expected values. Like other MCMC methods, it’s usually used for multidimensional problems, it can theoretically be used for unidimensional problems as well. However, easier methods are available for unidimensional problems, like adaptive rejection sampling.
How Does It Work?
The Metropolis-Hastings algorithm follows a four step process: initialization, generation of candidate samples, acceptance/rejection of candidate samples, and convergence to the target probability distribution. The first step involves selecting an initial sample point from which to begin the process; this can be any value within the range of possible values for the desired variable(s). After an initial sample point has been chosen, candidate samples are generated based on a proposal distribution; this is typically done using some form of random selection or perturbation of existing values. These candidate samples are then evaluated against the target probability distribution to determine whether they should be accepted or rejected; samples with higher likelihoods are more likely to be accepted than those with lower likelihoods. Once sufficient sample points have been accepted, they can be used to create an accurate model of the desired probability distribution.
The basic steps for the Metropolis algorithm (from Gelman et. al) are:
- Choose a starting point θ0 from a starting distribution, where p(θ0|y) > 0. This may be a very rough estimate.
- For all t values 1,2,…, sample a proposal θ* from a “proposal distribution”, which must be a symmetric distribution. θ* is sampled at time t, Jt( θ*| θt-1)
- Calculate the density ratio:
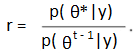
- Set:
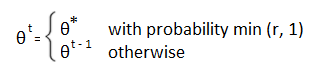
A Simple Explanation of the Steps
The above steps can be a little difficult to wrap your head around if you’re new to Bayesian statistics and prior distributions. However, you can get a good idea of what’s involved by imaging you’re on vacation in Orlando. Your goal is to visit as many major tourist attractions as possible, maximizing your time at major attractions and minimizing your time at unpopular locales. From your starting point (let’s say it’s a theme park you think could be popular), you have to decide if you are going to:
- Stay at your current location,
- Move to the nearest westerly attraction, or
- Move to the nearest easterly attraction.
Unfortunately, you lost your guide book and your cell phone. So you have no idea which attractions are the most popular, nor do you know how many attractions there are. That said, you do have a starting point, so you can ask the theme park office how many visitors they get each day. As you’re a bit at a loss of where to go next, you toss a coin. Heads, you go west. Tails, you go east. For this example, you flip tails. You hop over to the next attraction to the east in record time and ask the office how popular the attraction is. If the new attraction (a.k.a. the proposal distribution) is more popular, you stay there. If it’s less popular, you’re going to figure out the probability of moving based on the popularity of your current location (pcurrent) and the popularity of your proposed location (pproposed), which is:
pmove = (pproposed) / (pcurrent)
You fashion a crude circular spinner from a paper plate and straw from a fast food restaurant, marking values from zero to 1 on the outside of the plate. You spin the plate and note the number of the edge of the plate. If the value is between zero and pmove, you move. Anything else, you stay.
The above seems simplistic, but it does work: the probability that you are at any one attraction matches the relative number of visitors to that attraction. (Adapted from Kruschke, 2010).
Metropolis Algorithm vs. Metropolis-Hastings Algorithm
The Metropolis algorithm is a special case of the general Metropolis-Hastings algorithm (Hoff, 2009). The main difference is that the Metropolis-Hastings algorithm does not have the symmetric distribution requirement (in Step 2 above). If you do use an symmetric distribution, an adjustment to R (Step 4) must be made (Gelman, 2013):
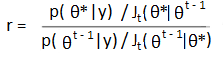
The Metropolis algorithm can be slow, especially if your initial starting point is way off target. Using asymmetric proposal distributions (i.e. using the more general Metropolis-Hastings Algorithm) can speed up the process.
References
Gelman, A. et al. (2013). Bayesian Data Analysis, Third Edition. CRC Press.
Hastings, W. (1970). “Monte Carlo sampling methods using Markov chains and their application.”
Biometrika, 57: 97–109.
Hoff, P. (2009). A First Course in Bayesian Statistical Methods. Springer Science and Business Media.
Kruschke, J. (2010). Doing Bayesian Data Analysis: A Tutorial Introduction with R. Academic Press.
Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. (1953). “Equations of State Calculations by Fast Computing Machines”. Journal of Chemical Physics. 21 (6): 1087–1092.