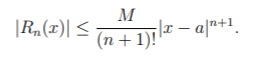Taylor series can be very good approximations for functions, but sometimes the errors (the difference between the original function and the Taylor approximation) can be large. A way to quantify this error is to use Taylor’s Inequality. It tells us how good our Taylor approximation is.
Formal Definition of Taylor’s Inequality
Formally, Taylor’s inequality states that [1]:
If |f(n + 1)(x) | ≤ M for |x – a| < R, then the remainder Rn(x) of the Taylor series satisfies
Taylor’s inequality estimates the error of a Taylor approximation as a function of the order of the Taylor polynomial, n.
M bounds the next derivative of the function. There are several ways to calculate M. Which you use depends on what kind of function you have. For example, sine functions and cosine functions are easy to bound because the derivatives alternate between sin(x) and cos(x). All sine and cosine functions have maximum outputs of 1, so M = 1. For other functions, you can optimize the function, taking the derivative and setting it equal to zero to find the critical points; in some cases, if the function is strictly increasing or decreasing, the maximum will occur at the endpoints.
Taylor’s Inequality Worked Example
The following graph shows a MacLaurin polynomial 1 + x + (1/2 x2) + (1/6 x3)+ (1/24 x4), which approximates the function f(x) = ex:
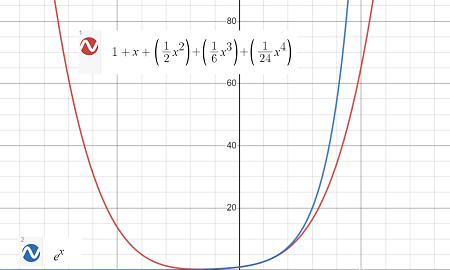
Question: How good is the approximation for the closed interval [−4, 4]?
Solution:
This is a fourth degree polynomial, so the “next” derivative is the fifth derivative. We know that f(5) ex = ex, so |f(5) ex| < ex if |x| < 4.
For |x| < 4, plugging our values into the Taylor’s inequality formula we get [3]:
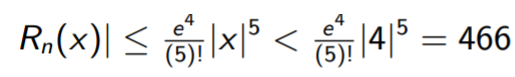
The remainder is an upper bound for the error. It’s not possible to find an exact value for the remainder.
References
Graph: Desmos.com
[1] Lahodny, G. (2019). Section 10.9: Applications of Taylor Polynomials. Retrieved July 21, 2020 from: https://www.math.tamu.edu/~glahodny/Math152/Section%2010.9.pdf
[2] Dedford, D. Taylor Polynomials. Retrieved April 3, 2021 from: https://people.csail.mit.edu/ddeford/Taylor_ERROR.pdf
[3] Applications of Taylor Series. Retrieved April 3, 2021 from: https://www3.nd.edu/~apilking/Math10560/Lectures/Lecture%2033.pdf