Talbot’s curve takes on a few different shapes. For example, one curve looks like a football, another looks like a mirrored fish tail:
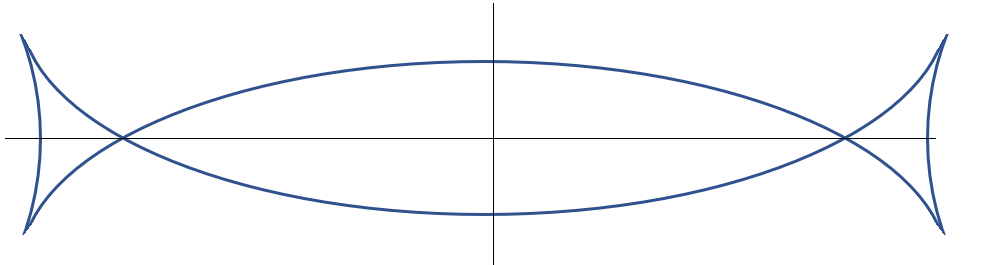
The above curve has four cusps and two ordinary double points (nodes), which will happen any time the eccentricity (the fraction of the distance to the semimajor axis where you’ll find the focus) of the ellipse is > 1/√2 [1].
Equations for Talbot’s Curve
Talbot’s curve is the negative pedal curve (a particular kind of locus*) of an ellipse with respect to its center O. The parametric equations for Talbot’s curve are [2]:

Alternate definitions exist, including one given by the Suffridge polynomial [3]:
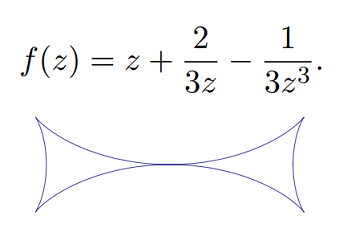
*More specifically, a pedal curve is the locus of the feet of the perpendiculars from the point to the tangent lines; it is a way to derive a new curve based on a given curve (in this case, the ellipse) and a point. The negative pedal curve is the inverse of the pedal curve.
History of Talbot’s Curve
The curve is named after Henry Fox Talbot (1800 to 1877) who first investigated it.
An early definition appeared on page 171 of the 1857 Proceedings of the Royal Society [4]:
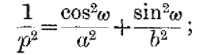
The curve, for the most part, fell into obscurity. In the 1902 Proceedings of the Annual Convention of the American Railway Engineering Association, the following remark was made about the Talbot curve: “It is used to some extent in this country” and “it is a very good curve.” Although there were arguments from committee members to merge the curve into a general family of spiral curves (this particular measure was not passed).
References
[1] Talbot’s Curve. Retrieved March 5, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/t/t020.htm
[2] Kokosa, S. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Retrieved March 5, 2022 from: http://facstaff.bloomu.edu/skokoska/curves.pdf
[3] Lee, S. & Makarov, N. (2014). Sharpness of connectivity bounds for quadrature domains from https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.760.8945&rep=rep1&type=pdf
[4] Cayley, Proceedings of the Royal Society (1857-9), cited in Greenhill, A. (1892). THE APPLICATIONS OF ELLIPTIC FUNCTIONS (PDF). Macmillan and Company.