Abel’s test (also called Abel’s Uniform Convergence Test) is a convergence test for infinite series; An infinite series is formed by adding up all of the terms in an infinite sequence of terms. This test tells us whether some infinite series converges—settles on a certain number—in certain situations.
It was named after Niels Henrik Abel(1802-1829), a Norwegian mathematician who provided a proof of the test.
There are two versions of the test.
- Real analysis, which deals with series of real numbers,
- Power series in complex analysis.
Several variants exist within those spheres, possibly because several notable mathematicians (including Abel, Dirichlet, and Dedekind) worked on similar theories at the same time. You can find many more variants on page 378 and in the exercises for that chapter of Elementary Real Analysis.
Version 1: Abel’s Test in Real Analysis
One of the more simple versions is stated as follows:
If
- Σ an is a convergent series, and
- bn is a monotonic series, and
- bn is a bounded series,
then Abel’s test tells us that the series Σ anbn is also convergent.
The CRC Concise Encyclopedia of Mathematics gives a slightly different list:
Let’s suppose that {un(x)} is a sequence of functions. If the following are true, the series Σ {un(x)} converges for all x ∈ [a, b]:
- un(x) can be rewritten as anfn(x),
- Σan is convergent,
- f(x) is monotonically decreasing,
- f(x) is bounded for some region.
The difference between the two lists are the specification that the series can be rerwitten, and that the function is monotonically decreasing. Elementary Real Analysis seems to agree with the shorter list (“Abels’…required the sequence…to be convergent and monotone”), but as noted above: several variants exist so keep this in mind if you’re using this particular test.
Version 2: Complex Analysis
The second version of Abel’s test is very similar, and is especially handy when you need to show that a power series is convergent on the boundary of its circle of convergence (the largest disc on which the series converges).
It tells is if a sequence of positive numbers—call it an—is decreasing monotonically (at least for all n greater than a natural numbers m), and if we know that the limit of an is zero as n goes to infinity, then the power series:
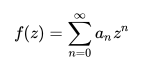
converges everywhere on the closed unit circle where z ≠ 1. A unit circle is a circle with a radius of one, and “closed” means the boundary is included.
This test gives us no information about the case when z = 1. If you need to evaluate that case you will have to use a different test.
References
Morrow, Jim. Abel’s Test. University of Washington Math Department. Published Feb 9, 2011. Retrieved from https://sites.math.washington.edu/~morrow/335_12/Abel.pdf on March 23, 2019.