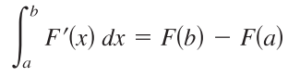The net change theorem gives you a way to place a value on a changing quantity. It is stated formally as [1]:
The definite integral of the rate of change of a quantity F′(x) gives the net change (or total change) for the quantity on the interval [a, b].
To put this another way, a function’s net change is the definite integral of it’s derivative.
A special case of the theorem relates an object’s position function s(t) and its rate of change v(t). Distance traveled is an object’s final position minus its initial position—the integral of velocity [2].
Net Change Theorem Example
Example question #1: Water flows into a lake at a rate of 8 + 3t gallons per minute, where 0 ≤ t ≤ 60. How much water flows into the lake in the first 20 minutes?
Step 1: Insert your values into the formula. From the question, we know that the limits of integration are 0 to 20. We’re also given the function to put into the formula: 8 + 3t:
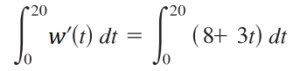
Step 2: Integrate using the usual rules for integration. This one uses the integral rule for power functions:
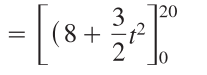
Step 3: Evaluate the formula. To do this:
- Plug your lower limit of integration (0) into the formula and solve. That equals zero for this problem.
- Plug your upper limit of integration (20) into the formula and solve. Plugging in 20 and solving gives 3600 + 600 = 4200.
- Subtract (1) from (2): 4200 – 0 = 4200.
The net change of water flowing into the lake in the first 20 minutes is 4200 gallons.
Example question #2: If an ball’s velocity function is v(t) = t2 – 6t + 8, what is the ball’s displacement between t = 0 and t = 5?
Step 1: Insert your values into the formula.
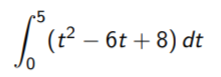
Step 2: Integrate using the usual rules for integration.
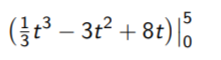
Step 3: Evaluate the formula.
(⅓(53) – 3(52) + 8(5)) – (⅓(02) + 8(0))
The solution is 20/3.
References
[1] Larson, R. & Edwards, B. (2009), Calculus, 9th Edition. Cengage Learning.
[2] Net Change Theorem. Retrieved April 12, 2021 from: https://web.ma.utexas.edu/users/m408s/AS/LM5-4-6.html