The continuity test is a set of three conditions that tell you whether a function is continuous at a specific point.
A function is continuous at an x-value of “c” if all of the following conditions are true:
- The function is defined at c: In other words, if you put the “x” value into the function, you’ll get a real value and not, for example, division by zero or something else that’s undefined.
- The function approaches the same value from the left and the right. In other words, the limit from above and the limit from below are in agreement.
- The function approaches the value f(c) from left and right. This is slightly different from #2, which just asks if they approach the same value. This condition states that the “same value” in condition 2 is the value you get when you plug the x-value into the function. In other words, conditions 1 and 2 should equal the same y-value.
Continuity Test Examples
Example question: Is the function f(x) = 3x2 + 7 continuous at x = 1?
Solution: Check the three conditions given in the definition.
- Is the function defined at c? Replace “x” in the formula to give:
f(x) = 3(12) + 7 = 10. Yes, the function is defined at x = 1. - Does the function approach the same value from the left and the right?. There are a couple of ways to check this:
- Graph the function and check to see if both sides approach the same number.
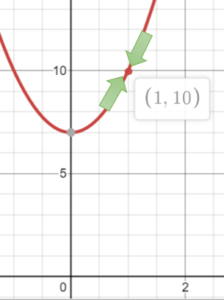
Approaching x = 1 from both sides, both arrows point to the same number (y = 10).
This graph shows that both sides approach f(x) = 16, so the function meets this part of the continuity test. - You can also create a table of values for small increments close to x = 1:
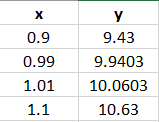
The numbers in the table are getting close to 10 from both sides (from the negative and positive directions).
- Graph the function and check to see if both sides approach the same number.
- Does the function approach the value f(c) from above and below? In this step, compare the values from Step 1 and Step 2 above. Yes, the two sides meet at y = 10.
This function has passed the continuity test. We can conclude that the function is continuous.