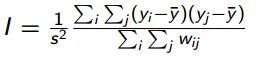Moran's I: Definition, Examples

What is Moran’s I?

Moran’s I is a correlation coefficient that measures the overall spatial autocorrelation of your data set. In other words, it measures how one object is similar to others surrounding it. If objects are attracted (or repelled) by each other, it means that the observations are not independent. This violates a basic assumption of statistics — independence of data. In other words, the presence of autocorrelation renders most statistical tests invalid, so its important to test for it. Moran’s I is one way to test for autocorrelation.

Spatial autocorrelation is multi-directional and multi-dimensional, making it useful for finding patterns in complicated data sets. It is similar to correlation coefficients, it has a value from -1 to 1. However, while other coefficients measure perfect correlation to no correlation, Moran’s is slightly different (due to the more complex, spatial calculations):

-1 is perfect clustering of dissimilar values (you can also think of this as perfect dispersion).
0 is no autocorrelation (perfect randomness.)
+1 indicates perfect clustering of similar values (it’s the opposite of dispersion).

Perfect Dispersion

In the above image, the black and white squares have a definite pattern and are perfectly dispersed. The Moran’s value would equal -1.

Perfect Randomness

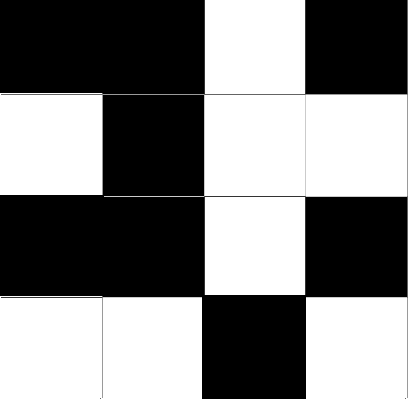
If the squares were truly randomly dispersed, the Moran’s value would be 0.

Perfect Clustering

This image shows that the white squares and black squares occupy one half of the area, either side of the center. This is perfect clustering of similar values, which gives a Moran value of +1.

Evaluating the Index

Moran’s I is unlike most other correlation coefficients in that you can’t take the index at face value. It is an inferential statistic, and you have to determine statistical significance before you can read the result. This is done with a simple hypothesis test, calculating a z-score and its associated p-value.

The null hypothesis for the test is that the data is randomly disbursed.
The alternate hypothesis is that the data is more spatially clustered than you would expect by chance alone. Two possible scenarios are:
1. A positive z-value: data is spatially clustered in some way.
2. A negative z-value: data is clustered in a competitive way. For example, high values may be repelling high values or negative values may be repelling negative values.

Calculations

Calculations for Moran’s I are based on a weighted matrix, with units i and j. Similarities between units is calculated as the product of the differences between y_i and y_j with the overall mean.

Similarity = (y_i – ̄y)(y_j – ̄y), where ̄y = Σⁿ_i=1 y_i/n
The Moran’s statistic is calculated using the basic form, which is divided by the sample variance:s² = (Σ(y_i– ̄y)²)/n).