The monotone likelihood ratio (MLR) represents a useful data generating process; one where there’s a clear relationship between the magnitude of observed variables and the probability distribution they are drawn from. This clear relationship makes many statistical processes possible, including identifying uniformly most powerful processes.
The MLR is defined as follows:
If the ratio of the two probability density functions, f(x) and g(x) meets the following requirement, they have the monotone likelihood ratio property:
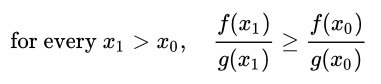
The ratio never decreases for all X.
Phraseology
If, with respect to just a particular argument x, two functions fulfil the condition above, we would say “they have the monotone likelihood ratio property in x”. When a family of distributions all have monotonic likelihood ratios with respect to a statistic T(X), we would say that family ‘has the MLR property in T(X)’.
Families of Distributions Which Satisfy the MLR
The following families satisfy the monotone likelihood ratio property for the statistic T(X)= Σ:
- Exponential distributions [λ]
- Binomial distributions [n, p],
- Poisson distributions [λ],
- Normal distribution [μ, σ] if σ is known.
Significance of the Monotone Likelihood Ratio Property
The MLR property is important in areas like: probability models, hypothesis testing, and point estimation. This property is also used to derive Uniformly Most Powerful (UMP) tests for hypothesis testing. A UMP is a test which has the greatest power among all possible tests of a given size; and so determining which it is in a given circumstance can be very important.
References
- Monotone Likelihood Ratio. Statistics for Applications: Fall 2003 Lecture Notes. https://ocw.mit.edu/courses/mathematics/18-443-statistics-for-applications-fall-2003/lecture-notes/lec21.pdf on May 3, 2018.
- Mukherjee, Shirsendu. Statistical Inference I: Monotone Likelihood Ratio. Retrieved from http://epgp.inflibnet.ac.in/epgpdata/uploads/epgp_content/S000034ST/P001013/M020980/ET/1499856024Module-31.pdf on May 3, 2018
- Watkins, J. Uniformly Most Powerful Tests. Retrieved from http://math.arizona.edu/~jwatkins/ump.pdf on May 3, 2018.