Statistics Definitions > Mean Error
What is Mean Error?
The mean error is an informal term that usually refers to the average of all the errors in a set. An “error” in this context is an uncertainty in a measurement, or the difference between the measured value and true/correct value. The more formal term for error is measurement error, also called observational error.
Why It’s Seldom Used
The mean error usually results in a number that isn’t helpful because positives and negatives cancel each other out. For example, two errors of +100 and -100 would give a mean error of zero:
Zero implies that there is no error, when that’s clearly not the case for this example.
Use the MAE Instead!
To remedy this, use the mean absolute error (MAE) instead. The MAE uses absolute values of errors in the calculations, resulting in average errors that make more sense.
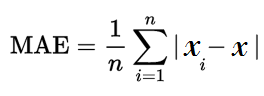
The formula looks a little ugly, but all it’s asking you do do is:
- Subtract each measurement from another.
- Find the absolute value of each difference from Step 1.
- Add up all of the values from Step 2.
- Divide Step 3 by the number of measurements.
For a step by step example, see: mean absolute error.
Other Terms that are Very Similar
While the “mean error” in statistics usually refers to the MAE, it could also refer to these closely related terms:
- Mean absolute deviation (average absolute deviation): measures the average standard deviation, which is a spread of values around the center of a data set. The terms sound similar, but they have practically nothing to do with each other because a standard deviation is a unit of spread and an error is a difference in unit measurements.
- Mean squared error: used in regression analysis to show how close a regression line is to a set of points. “Errors” in this context are distances from the regression line.