Mallows’ Cp Criterionis a way to assess the fit of a multiple regression model. The technique then compares the full model with a smaller model with “p” parameters and determines how much error is left unexplained by the partial model. Or, more specifically, it estimates the standardized total mean square of estimation for the partial model with the formula (Hocking, 1976):
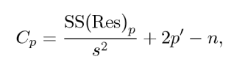
Where:
- SS(Res)p = residual sum of squares from a model with a set of p – 1 explanatory variables, plus an intercept (a constant),
- s2 = estimate of σ2
A common method is to perform all possible regressions, then use Mallows’ Cp to compare the results.
How to Interpret Mallows’ Cp
Various suggestions have been made as to exactly how the statistic should be interpreted, but the general consensus is that smaller Cp values are better as they indicate smaller amounts of unexplained error. That said, the statistic should be used in context, based on your field and knowledge of the data. Like any model fitting method, the “best” model isn’t necessarily a “reasonable” model.
A plot of Cp versus p (a constant) can also help you compare models; You may want to only consider models that have a small Cp and a Cp close to p. Alternatively, you may want to choose the smallest model for which Cp ≤ p is true.
Alternate ways to assess fit include R2 and adjusted r-squared. These are often used in conjunction with Mallows’ Cp to assess model fit. Another alternative, Akaike’s Information Criterion (AIC) is equivalent to Mallows’ Cp for Gaussian linear regression (Boisbunon, 2013).
References
Boisbunon, A. et al. (2013). “AIC, Cp and estimators of loss for elliptically symmetric distributions”. arXiv:1308.2766 [math.ST].
Gilmour, S. The Interpretation of Mallows’s $C_p$-Statistic. Journal of the Royal Statistical Society. Series D (The Statistician). Vol. 45, No. 1 (1996), pp. 49-56
Hocking, R. The Analysis and Selection of Variables in Linear Regression. Biometrics, 32:1-49.
Hobbs, G. Model Building: Selection Criteria. Retrieved March 5, 2020 from: https://www.stat.purdue.edu/~ghobbs/STAT_512/Lecture_Notes/Regression/Topic_15.pdf