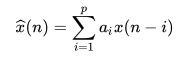Linear prediction is a technique for anlayzing time series; It allows us to predict future values from historical data. It is often used in digital signal processing, because it allows the future values of a signal to be estimated in terms of a linear function of past samples.
Types of Linear Prediction
There are three main types of linear prediction. They are differentiated by the form of the transfer function; a function H(Z) which can generally be defined according to its characteristics:
- The numerator of H(z) is constant: We call this an autoregressive (AR) or all-pole model.
- The denominator of H(z) is constant: This we call a moving average or all-zero model.
- No assumptions can be made about the characteristics of H(z): A model in which we can make no assumptions is called a autoregressive moving average (ARMA), or mixed pole/zero model.
Calculating Predicted Signal Values
The autoregressive model is the model most extensively and used and studied today. This is because of a couple of reasons:
- It produces equations that are relatively easy to solve,
- It accurately models many practical, real world applications, such as speech production.
In the autoregressive model, a predicted signal value x̂(n) can be calculated by:
- x(n-i) are the previous observed values,
- ai are the predictor variable’s coefficients.
This is an estimate; not an exact value, and the error term is referred to as e(n). By definition, where x(n) is the true signal value,
e(n)= x(n) – x̂(n)
References
Cinneide, Alan. Linear Prediction. The Technique, Its Solution and Application to Speech. Retrieved from https://www.dit.ie/media/electricalengineering/documents/mikelgainza/92.pdf on May 16, 2018.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Mahkonen, Katariina. Linear Prediction. SGN-14006 Course Notes. Retrieved from http://www.cs.tut.fi/~sgn14006/PDF/S03-LP.pdf on May 16, 2018.
Vaidyanathan, P. P. The Theory of Linear Prediction. Retrieved from https://authors.library.caltech.edu/25063/1/S00086ED1V01Y200712SPR003.pdf on May 14, 2018.