Kriging is a type of regression that gives a least squares estimate of data (Remy et. al, 2011). It uses z-scores to generate an estimated surface model from the spatial description of a scattered set of data points. It originated in mining geology, and is now an important part of the geostatistics toolbox. It also has applications in computer engineering, remote sensing, and environmental science.
One strong point of this type of interpolation is that it not only generates an interpolated spatial model, it also generates an estimate of the uncertainty of each point in that model.
Unlike linear regression or inverse distance weighted interpolation, kriging interpolation is based primarily on empirical observations, the observed sample data points, rather than on a pre-assumed model.
The interpolation gives more weight to sample points nearby a location than those further, and, in order to reduce sampling bias, weighs clusters less heavily than single points. The value of each point is calculated in such a way as to minimize the expected error for that particular point.
Example
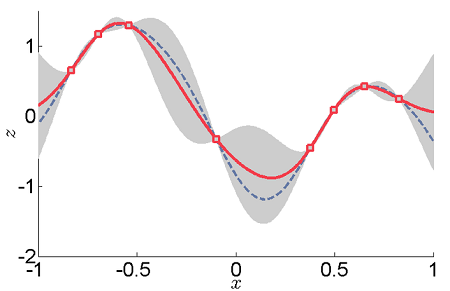
The above graph is an example of one-dimensional data interpolation by kriging.
- The gray areas are the normally distributed confidence intervals.
- The red line represents the kriging interpolation, which runs along the means of the normally distributed confidence intervals.
- Squares show the original data points.
- The dashed curve shows a smooth spline. However, this departs significantly from the expected intermediate values given by the means.
Limitations of Kriging Interpolation
Kriging assumes that the space being studied is stationary; that is to say, that the joint probability distribution doesn’t change throughout the study space.
It also assumes a property called isotropy; that there is uniformity in every direction.
If these conditions are difficult to fulfill, the method becomes problematic. However, in universal kriging the stationary requirement is relaxed.
The accuracy of your model will be limited if the data aren’t spatially correlated, if their limited in spread, or if the number of data points are small.
References
- ArcMap Documentation. Retrieved from http://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-kriging-works.htm on June 24, 2018
- Clark, I. What is Kri-ging Anyway? Retrieved from http://www.kriging.com/whatiskri-ging.html on June 24, 2018
- GIS Geography. The Prediction Is Strong in this One. (How to Interpolate With Geostatistics) Retrieved from https://gisgeography.com/kriging-interpolation-prediction/ on June 24, 2018
- Population Health Method. Retrieved from
https://www.mailman.columbia.edu/research/population-health-methods/kri-ging on June 24, 2018. - Remy et. al (2011) Applied Geostatistics with SGeMS: A User’s Guide. Cambridge University Press.