Put simply, the sum of a series is the total the list of numbers, or terms in the series, add up to. If the sum of a series exists, it will be a single number (or fraction), like 0, ½, or 99.
The problem of how to find the sum of a series has been around since ancient times. Archimedes’ summation of 1 + 1/4 + 1/42 + … was one of the earliest examples. Some summations were tougher than others; the first “really tough” summation problem was 1 + (1/2)2 + (1/3)2 + …, which Mengoli, and brothers Jakob Bernoulli and Johann Bernoulli tackled without success. It was Euler who found the solution (π2/6) in 1734, long after Jakob Bernoulli had died [1].
How to Find the Sum of a Series: General Steps
In most cases, it isn’t possible to calculate the exact sum of a series. In fact, it is extremely challenging to know the exact sum of most infinite series. However, there are a couple of exceptions [2]:
- The geometric series:
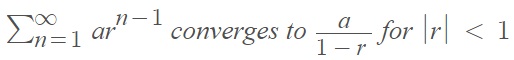
- The telescoping series:
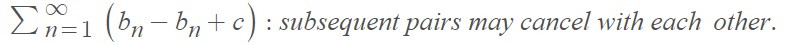
For other series, a little legwork is involved. A first step is to use a computer to see where the sum might be headed. You could try the first thousand terms, of the first 10,000 terms (or use one of the various calculators you can find online!). This might work well if you have computer and patience, but it won’t tell you if the solution you get is the “best.”
How to Find the Sum of a Series with Partial Sums
You can estimate the sum of a series with partial sums. If the limit of an infinite series exists and is finite, that limit is also the sum of an infinite series. So, if we find the limit of its sequence of partial sums, we can find the sum of a series. The idea is that you can find the sum of the series as a whole by finding the sum of small “partial” pieces of the sum. The more parts you include, the closer you get to the limit of the sequence of partial sums. Like the “adding up terms” approach outlined above, this isn’t always a very practical approach. A better way is to use partial sums in conjunction with the integral test and remainder theorem.[3]
In order to use this method, first run the integral test and verify that the series converges. The test will give you a remainder value, which represents the error when approximating the infinite summation of series to the nth partial sum. The remainder, Rn is the difference between the true sum of the series and the one you get with n partial sums:
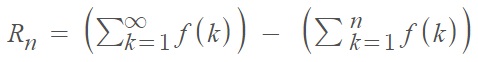
The more partial sums you use, the better the approximation and the smaller the remainder. This means that this is a nonincreasing function, which can be described by integrals shown in the following graphs:
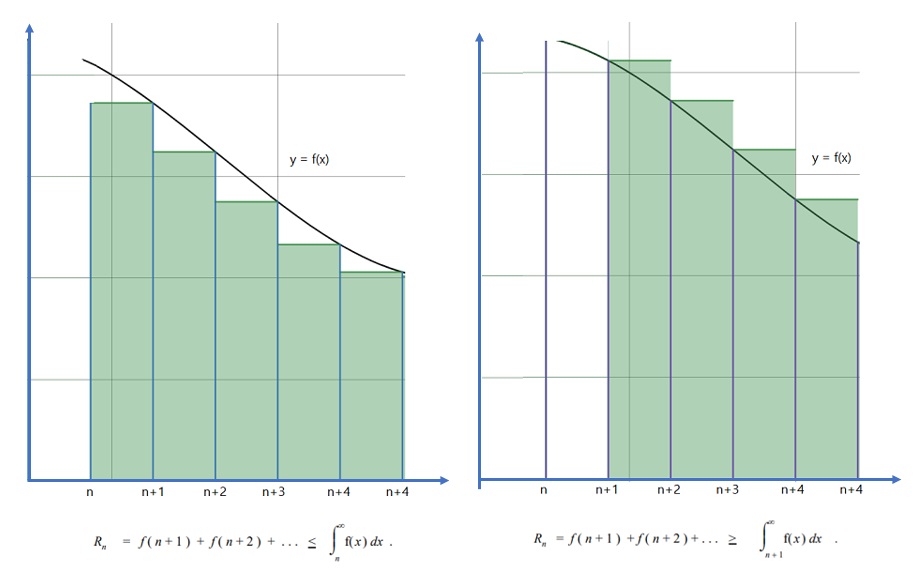
The result is the remainder theorem [3]:
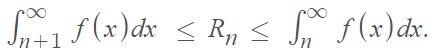
The theorem is valid for a series that converges by the integral test, with the remainder
Rn = S – sn, where:
- S is the sum of the series
- sn is the sum obtained with partial sums.
Adding sn to both sides of the equality gives:
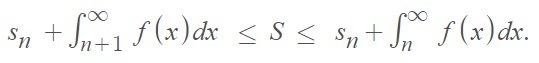
Note: Use caution when interpreting convergence tests. Not all convergence tests help you find the sum of a series. For example, the root test and ratio test involve taking a limit. While they can tell you something about convergence, they say nothing about the value of the sum [4].
How to Find the Sum of a Series: Example
Example question: Estimate the sum of the following series with the 10th partial sum:
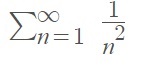
Step 1: Run the integral test to confirm convergence. This function passes that test.
Step 2: Apply the Remainder Theorem:
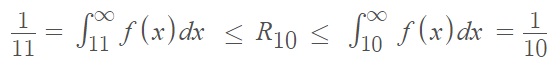
Adding s10 to each side gives:
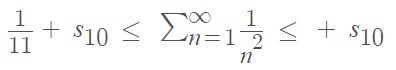
Where the tenth partial sum is:
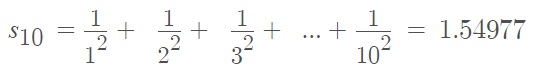
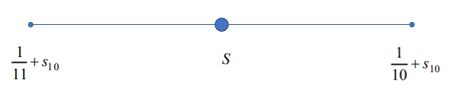
Step 3: Use the information from Step 2 to estimate S, which is going to be the mean of the upper and lower bounds:
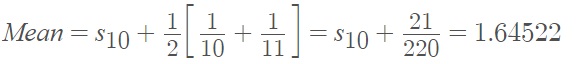
References
[1] Stillwell, J. (2010). Mathematics and Its History. 3rd Edition. Springer.
[2]Heap, A. Series Summary. https://www.geneseo.edu/~heap/courses/222/series_review.pdf
[3] Maslanka, D. The Integral Test and Remainder Theorem.
http://mypages.iit.edu/~maslanka/LN7.pdf
[4] Foy, C. (2013). Situation 1. Retrieved August 18, 2021 from: http://jwilson.coe.uga.edu/EMAT6500/ClassSit/Foy/situation1.pdf