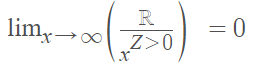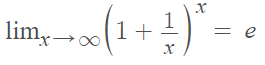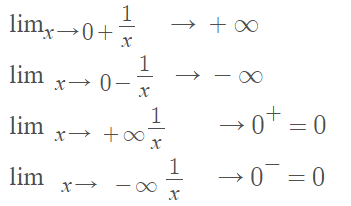Limits >
Special limit theorems are a set of rules to evaluate certain limits. They are “special” because they tackle limits that can’t easily be evaluated by any of the usual methods. In a way, they are shortcuts to dealing with specific forms of limits.
List of Special Limit Theorems
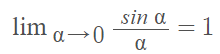
This limit for sin can only be used when approaching zero. α can be any number.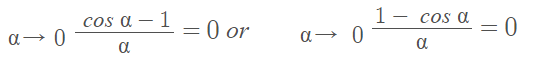
This limit for cos can only be used when approaching zero.
ℝ is any real number; Z is an integer.
e is Euler’s number. An alternative way of defining e as a limit is [1]:
Both of these are stating the same things: when you raise 1 (plus a miniscule number)to a very large power, that will eventually equal Euler’s number.
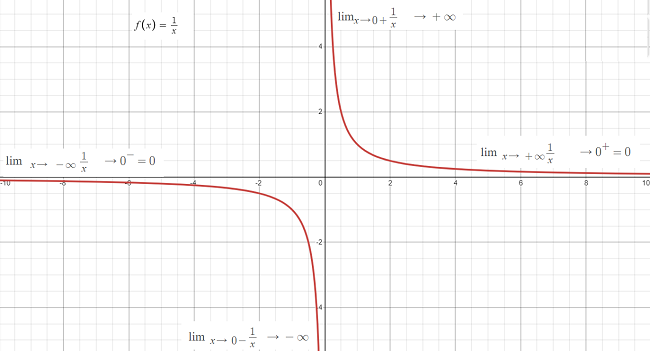
Four ways to find limits for 1/x.
These are all basic facts about the behavior of functions. For example, if you look at a graph of 1/x, you can see where the function tends to zero, or infinity:
Examples
Example question: Evaluate the limit using a special limit theorem:
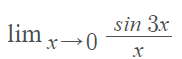
Step 1: Get the limit expression into one of the special limit forms given above. In order to use the first special limit theorem, we have to multiply by 3/3:
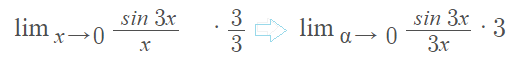
Step 2: Evaluate the individual parts:
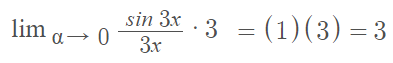
That’s it!
Special Limits for Polynomials
Finding limits for polynomials can seem overwhelming, especially when you’re faced with an ugly looking equation like this one:
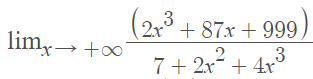
However, polynomial limits are special because you can ignore every term, except for the one with the highest power (e.g. the highest degree term). In this expression, the terms with the highest degree power are raised to the third power. If we eliminate everything else except the 3rd degree terms, we get:
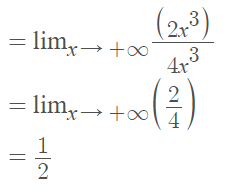
References
[1] Special Limits. Definition of e. Retrieved July 12, 2021 from: https://homepages.math.uic.edu/~rmlowman/math165/LectureNotes/L4-W2L1speciallimits.pdf
One-Sided and Infinite Limits. Retrieved July 12, 2021 from: https://www.lcps.org/cms/lib/VA01000195/Centricity/Domain/10242/L6_One%20Sided_Infinite%20Limits.pdf