The Wallis formula is named after an English mathematician John Wallis (1616-1703), who is most famous for his work on a method of interpolation which expanded on Cavalieri’s method of indivisibles. Wallis’ formula for π came decades before the advent of calculus and was seen as a remarkable, yet unbelievable result at the time [1]. The formula gives a simple infinite product expansion for π. In its most basic form, it can be stated as:
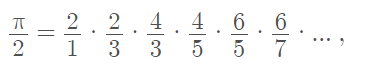
Equivalently, the formula can be stated in product notation as:
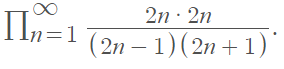
The formula, useful in many combinatorics and probability applications, is very slow to converge.
Other Forms of Wallis’s Formula
Pulling out every other pair of terms gives an interesting result:
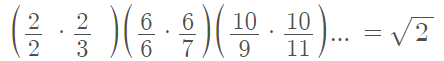
Since its discovery, the formula has been reworked and reformulated in a variety of different guises. For example, Leonhard Euler (1707-1783) rediscovered Wallis’s formula by substituting π/2 for x his infinite product [2]:
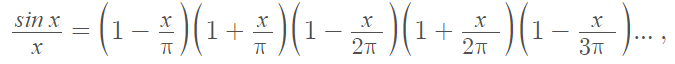
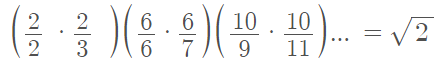
Another way of writing the formula is with limits and factorials:
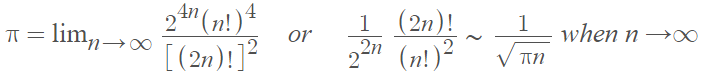
This particular way of writing the formula is important in combinatorics and probability theory [3].
Derivation of The Wallis Formula with Integrals
One infinite product formula for the sine function gives Wallis’ formula as a result (infinite products are the limits of partial products, which are finite) [4]. Wallis’ integrals works for definite integrals with integral bounds of [0 to π/2]. For example:
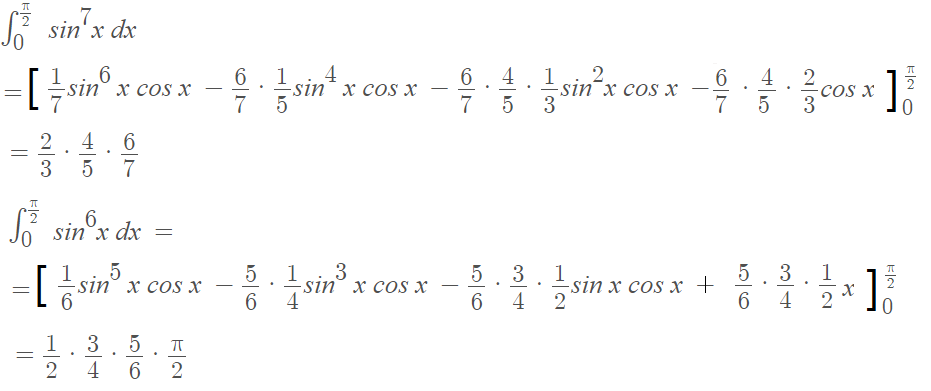
If you’re working with odd powers, you may get zero for some intervals. This is because results in different quadrants cancel each other out, in the same way that integrals cancel out if they are positive (above the x-axis) and negative (below the x-axis).
References
[1] Sandifer, E. (2007). How Euler Did It. Mathematical Association of America.
[2] Perkins, D. (2018). Phi, Pi, e and i. American Mathematical Society.
[3] Eymard, P. & Lafon, J. (2004). The Number [pi]. American Mathematical Society.
[4] Su, Francis E., et al. “Wallis’ Formula.” Math Fun Facts.