A contour integral is what we get when we generalize what we’ve learned about taking integrals of real functions along a real line to integrals of complex functions along a contour in a two-dimensional complex plane.
A contour is a loop around the negative x-axis:
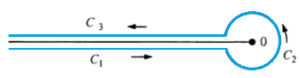
It’s not quite as difficult as it sounds. To directly calculate the values of a contour integral around a given contour, all we need to do is sum the values of the “complex residues“, inside of the contour. A residue in this case is what remains when you integrate around the origin. We can also apply the Cauchy integral formula, or use an application of the residue theorem.
What is a contour in the complex plane? Think about it as a finite (fixed) number of smooth curves. We can define it more exactly as a directed curve, that is made up of a finite sequence of directed smooth curves. Each of these curves must be matched to give just one direction.
Integrating a Contour Integral
Integrating over a contour might sound intimidating, so let’s start with something a bit simpler. Suppose we want to integrate the function f(x) over the curve Γ, and suppose M ∈ ℂ1[I] defines a curve such that Γ = M(I).
Then we can define contour integration over our curve Γ as
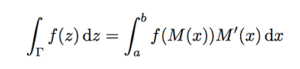
That’s all well and good. But what if we want to integrate over a contour which is defined by M1,…Ml ∈ C1[I]? We could describe our contour this way:
![]()
It turns out all that we need to do is define integration piecewise, and everything we’ve already learned carries over.
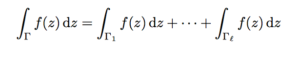
References
Chong, Y. D. MH2801 Course Notes: Complex Methods for the Sciences. Section 8, Contour Integration. Published 2016. Retrieved from
http://www1.spms.ntu.edu.sg/~ydchong/teaching/08_contour_integration.pdf on August 27, 2019
Olver, Sheehan. Class Notes: Lesson 8: Contour Integration Department of Mathematics, Imperial College. Retrieved from http://www.maths.usyd.edu.au/u/olver/teaching/NCA/08.pdf on August 27, 2019