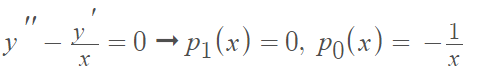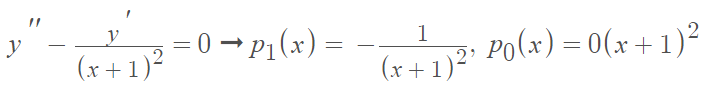Singular Point in Differential Equations
A differential equation of the form y′′ + p(x)y′ + q(x)y = 0 has a singular point at x0 if either of the following limits do not exist [1]:
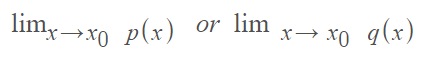
What this means for second order differential equations is that an initial value problem will not have a unique solution. Alternatively, it may not have any solution, or its solution or derivatives might be discontinuous. For linear homogeneous differential equations, a singular point happens when at least one coefficient is either undefined (i.e. discontinuous) or multivalued at that point [2].
Regular and Irregular Singular Point
Singular points can be regular or irregular. Regular singular points are well-behaved, defined in terms of ratios of the differential equation’s polynomial coefficients Q(x)/P(x) and R(x)/P(x) [3]. Irregular singular points exhibit bizarre behavior and cannot easily be pinned down or defined, other than to say that if a point isn’t regular, then it is irregular. To put this more concretely, a regular singular point can be defined as follows: It is where a singularity of P(x) is no worse than 1 / (x – x0) and the singularity of Q(x) is no worse than 1 / (x – x0)2. In other words, it’s where both of the following limits exist:
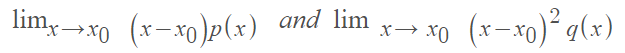
Otherwise, the point is an irregular singular point.
Examples of Regular and Irregular Singular Points
- Example of a regular single point x0 [4]:

Here, p2(x) is singular but xp0(x) = -1 is analytic* is x0 = 0 (and for all x). - Example of an irregular single point x0:

Here, x0 = -1 is an irregular singular point because (x + 1)p1(x) is singular at x = -1.
Example question: Are the singular points of (x3 − 3x2)y′′ + y′ + 2y = 0 regular or irregular?
Step 1: Find the singular points. As every coefficient is a polynomial, the singular points (0 and 3) are the roots of the leading coefficient, x3 – 3x2.
Step 2: Find the limits of each point.
x = 0 is an irregular singular point because the limit is undefined:
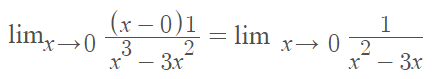
x = 0 is a regular singular point because both limits exist:
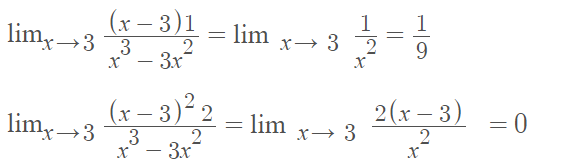
*Most functions you come across are “analytic.” All polynomial functions, rational functions, exponential functions, logarithmic functions, and trigonometric functions are analytic away from their singularities.
Singular Point in Complex Analysis
A singular point, also called a singularity, is a point where a complex function isn’t analytic. In other words, it’s an obstacle to analytic continuation where the function can’t be expressed as an infinite series of powers of z. Singular points can be classified as regular points or irregular points (also called essential singularities).
A singular point may be an isolated point, or a point on the curve (e.g. a cusp). If there aren’t any other singular points in the neighborhood of z, the point is called an isolated singularity. In some cases, you might be able to assign a value to the discontinuity to fill in the “gap”. If that’s the case, the point is called a removable singularity.
References
[1] Binegar, B. Lecture 19: Regular Singular Points and Generalized Power Series. Retrieved August 11, 2021 from: https://math.okstate.edu/people/binegar/4233/4233-l19.pdf
[2] Dobrushkin, V. MATHEMATICA TUTORIAL for the First Course. Part V: Singular and ordinary points. Retrieved August 11, 2021 from: https://www.cfm.brown.edu/people/dobrush/am33/Mathematica/ch5/singular.html
[3] 9.2. Classifying Singular Points as Regular or Irregular. Retrieved August 11, 2021 from: https://www.oreilly.com/library/view/differential-equations-workbook/9780470472019/9780470472019_classifying_singular_points_as_regular_o.html
[4] Bertherton, C. Regular and Irregular Singular Points of ODEs. Retrieved August 11, 2021 from: https://atmos.washington.edu/~breth/classes/AM568/lect/lect15.pdf