Calculus Definitions >
Contents:
What is a Manifold?
In beginning mathematics classes, you learn about two-dimensional surfaces and curves (like arcs or circles) or three-dimensional objects (like cones or spheres). In higher dimensional space, these curves and surfaces are called manifolds.
Simple Example of a Manifold in Mathematics
The definition of a manifold “…involves rather a large number of technical details” (Lee, 2006). But it’s possible to grasp the idea of a manifold without trudging through the depths of a technical definition, because the simplest higher-dimensional manifold in mathematics actually happens in three-dimensional space.
For example, the following image shows a single affine motion, a translation and rotation of a cone:
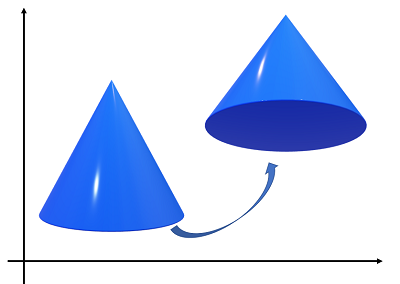
If you take the set of all possible affine motions in three-dimensional space, you get a six-dimensional manifold (Tu, 2010).
Dimension of a Manifold
The dimension of a manifold in mathematics is the number of parameters (i.e. independent numbers) needed to plot a point in space.
A line is a simple manifold of dimension 1. To plot the number 2 on a number line only requires one number: 2. Although a line isn’t “curved” in the usual sense of the world, it’s still considered a curve in the realm of manifolds. A graph of a continuous function also is a manifold of dimension 1.

Planes, spheres, cylinders and similar objects are manifolds of dimension 2. These manifolds are not the solid shapes but rather the skin that encloses the shape (like the surface of the Earth). For these shapes, two points (i.e. Cartesian coordinates) are needed to specify a point.
Any dimension above 3 is difficult or impossible to visualize. However, they still adhere to the same rule for the number of points. For example, a 7-dimensional manifold, modeled locally on ℝ7 (the doublestruck R is the set of all reals), would need 7 numbers to specify its location as long as it isn’t too far away from the starting point.
Covariant Derivative
A covariant derivative (∇x) generalizes an ordinary derivative (i.e. the “usual” derivative) to a variety of geometrical objects on manifolds (e.g. forms, tensors, or vectors).
More specifically, the covariant derivative is an operator that reduces to a flat space partial derivative with Cartesian coordinates; It transforms as a tensor on a random manifold and in fact, the essential feature of a covariant derivative is this tensor characteristic (Wempner, 1982). While the “usual” types of functions and vector fields are dealt with by ordinary differentiation, covariant derivatives specifically deal with differentiating tensors.
Covariant Derivative Defined More Simply
In (relatively) simple terms, the covariant derivative tells you how the “head” of a vector moves in relation to some movement of the vector’s “tail” in curved spacetime. A covariant derivative allows you to construct directional derivatives by just contracting with a vector. You don’t need to know its derivatives.
The covariant derivative is a rule that takes as inputs:
- A vector, defined at point P,
- A vector field, defined in the neighborhood of P.
The output is also a vector at point P.
Terminology note: In (relatively) simple terms, a tensor is very similar to a vector, with an array of components that are functions of a space’s coordinates. A manifold is a non-Euclidean space that, close up, looks Euclidean (i.e. flat).
References
Lee, 2006. Introduction to Topological Methods. Springer Science and Business Media.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 48-50, 1953.
Schmutzer, E. Relativistische Physik (Klassische Theorie). Leipzig, Germany: Akademische Verlagsgesellschaft, 1968.
Tu, L. (2010). An Introduction to Manifolds. Springer Science & Business Media.
Weinberg, S. “Covariant Differentiation.” §4.6 in Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, pp. 103-106, 1972.
Wempner, G. (1982). Mechanics of Solids with Applications to Thin Bodies. Springer Science & Business Media.
GR lecture 5 Covariant derivatives, Christoffel connection, geodesics, electromagnetism in curved spacetime, local conservation of 4-momentum