The term “differentiate by parts” is informal. Depending on the author, it could refer to:
- The Product Rule for Differentiation.
- Part of the process of integration by parts.
- Differentiating non-differentiable functions.
Most of the confusion about which procedure a particular author is referring to stems from the use of nonstandard notation. You may need to read any text that mentions “differentiating by parts” very carefully in order to decipher the author’s intent.
Differentiate by Parts #1: Products
For multiplied functions, finding the derivative can be a challenge. A fairly easy way to handle these types of functions is to break them into parts, applying the product rule. Most authors stick to using the letters fg for the product rule; Using the letters uv, plus referring to the procedure as “differentiate by parts”, leads to confusion with Integration by Parts (which also uses uv). However, some authors [e.g. 1, 2] use the nonstandard letters uv in the product rule formula:
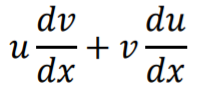
Despite the different letters, the procedure is exactly the same.
Example: Differentiate the following function with respect to x:
f(x) = x2 cos3x
Step 1: Split the function into two parts, labeling one part “u” and the other “v”:
- u = x2
- v = cos3x
Step 2: Find the derivatives for the two parts in Step 1:
- du/dx = 2x
- dv/dx = -3sin3x
Step 3: Insert your solutions from Step 1 and 2 into the formula:
(x2)(-3sin3x) + (cos3x)(2x)
That’s the solution, but you may want to rearrange it slightly into a more standard form:
-3x2sin3x + 2xcos3x
Differentiate by Parts #2: Integration by Parts
When some authors talk about “differentiate by parts” [3], what they are actually talking about is Integration by parts.
Integration by parts works when you want to integrate a product (multiplication) of two functions. For example, you would use integration by parts for ∫x · ln(x) or ∫ xe5x. As part of the integration process, you have to find derivatives of the two “parts”, as this formula shows:
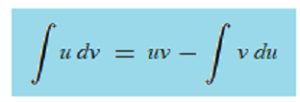
Essentially, “differentiate by parts” here means to find the individual parts of the function you’re trying to integrate. It might be less confusing to refer to this method as differentiating the parts!
Differentiate by Parts #3: Non Differentiable Functions
Some functions are not differentiable everywhere. For example, there might be a removable discontinuity in the function, or you could be dealing with a piecewise function. This means that you won’t be able to apply any of the “usual” derivative rules. The solution is the split the function up into one or more parts (which is easy to do with a piecewise function) and differentiate the separate pieces.
References
[1] Samori, P. (2006). Scanning Probe Microscopies Beyond Imaging. Manipulation of Molecules and Nanostructures. Wiley VCH.
[2] Robbins, A. & Miller, W. (2000). Circuit Analysis Theory and Practice · Volume 1. Delmar.
[3] Giordano, F. et al. (2013). A First Course in Mathematical Modeling. Cengage Learning. p. 642
You are bring too kind on stating that it might be less confusing to refer to the differentiation product rule as differentiation by parts as opposed to integration by parts. It’s akin to them calling division as addition.