A singular integral is where the integrand (the function being integrated) has an infinite value at one or more points within the given bounds of integration. This means that the integral cannot be evaluated using the traditional methods of integration, such as with Riemann sums or the trapezoidal rule.
Singular integrals appear in many areas, including fluid and solid mechanics and acoustic / electromagnetic wave scattering. They can be used to calculate the behavior of physical systems near singularities, such as the behavior of waves near a sharp point. They can also be used to calculate the behavior of mathematical functions near singularities, such as the behavior of the gamma function near infinity.
Singular Integral Classification
Formally, a one dimensional singular integral is defined as (Tran, 2017):
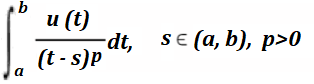
Singular integrals are classified by the order of singularity (a measure of the nature of unboundedness of the kernel).
- Weakly singular: p < 1. A value for the integral exists and is continuous at the singularity.
- Strongly singular: p = 1. The integrand and the integral are singular.
- Hyper-singular: p > 1.
An important class of singular integral is the one with a Cauchy kernel, which crops up in contact and fracture problems in solid mechanics. It is defined as (Mennouni, 2011):
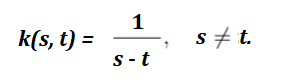
Singular Integral Equation
An integral equation of the form:
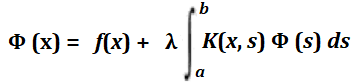
is singular if it has an infinite range of definition (for example 0 < x < ∞ or -∞ < x < ∞) or if the integral kernel isn’t square integrable (Moiseiwitsch, 2011).
Evaluating The Singular Integral
The usual numerical integration techniques often lead to inaccurate results. If an analytic solution can be found, they are usually difficult to solve—requiring an approximate solution. General steps for finding a solution:
- Remove the space containing the singularity and redefine the integral so that it has a solution,
- Take the limit of the remove space to find an approximate solution,
- Add both parts (1) and (2) for a total approximate solution.
Singular integrals can be evaluated using a variety of methods, such as the method of residues, the method of Cauchy integrals, and the method of Laplace transforms.
References
Hackbusch, W. (Ed.). (1991). Numerical Techniques for Boundary Element Methods, Proceedings of the Seventh GAMM Seminar held at the Christian-Albrechts Universität, Kiel, January 25-27.
Huang, Q. and Cruse, T. A. (1993). Some Notes on Singular Integral Techniques in Boundary Element Analysis. Int. J. Numer. Meth. Eng. 36, 2643-2659.
Mennouni, A. (2011). [For solving Cauchy singular integral equations]. General Mathematics
[math.GM]. Université Jean Monnet – Saint-Etienne, English. ffNNT : 2011STET4005ff. fftel00691919f
Moiseiwitsch, B. (2011). Integral Equations. Dover Publications.
Stein, E. M. Singular Integrals and Differentiability Properties of Functions. Princeton, NJ: Princeton University Press, 1971.
Tran, N. (2017). Simple Method for Evaluating Singular Integrals. Retrieved August 29, 2020 from: