A plane region is any area in two-dimensional space. Usually in calculus, we’re interested in evaluating bounded plane regions. A bounded plane region can be enclosed in a rectangular region:
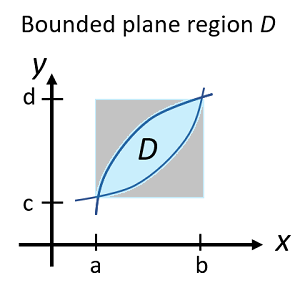
Area of a Plane Region
You can find the area of a plane region in a couple of different ways: with Riemann sums, where areas are calculated as explicit limits, or with definite integrals. Riemann sums will give you an approximation (sometimes a very good one), while definite integrals give you an exact solution. You can also find the Area by the limit definition.
Example question: What is the area of the region between f(x) = x2 – x + 2 and the x-axis on the closed interval [-1, 2]?
Option 1: Riemann Sums. This method gives us an okay approximation (A = 5.71) using n = 20 rectangles (this Desmos calculator provides the setup).
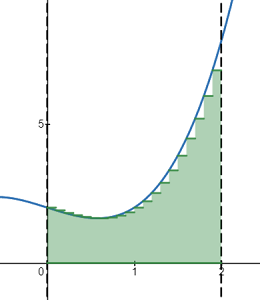
How good the approximation is depends on a few factors including the number of rectangles and whether you use a left or right hand Riemann sum or another variation (e.g. the midpoint rule). Theoretically, if you use an infinite number of rectangles, you’ll get an exact solution. This is the idea behind the next option: the definite integral.
Option 2:Definite Integrals: The exact solution, using definite integrals, is A = 6.
Type I and II Plane Region
There are two types of bounded plane regions [1, 2]:
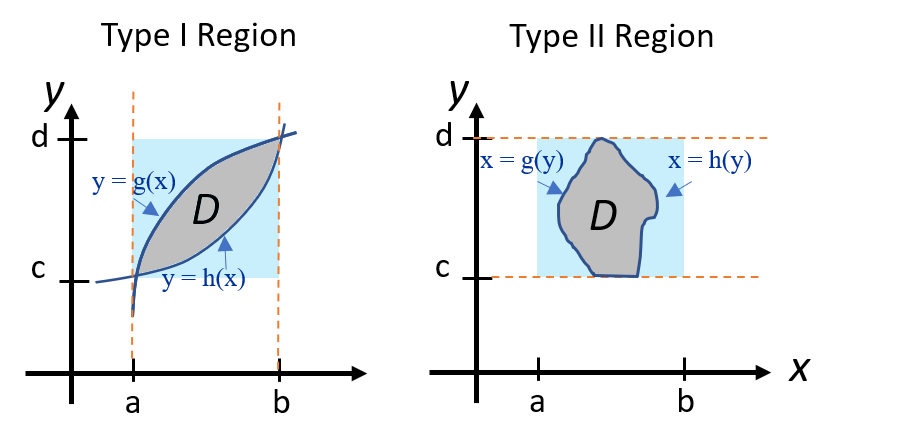
- Type I regions: bounded by two vertical lines x = a and x = b, and two curves y = g(x) and y = h(x),
- Type II regions: bounded by two horizontal lines y = c and y = d, and curves x = g(y) and x = h(y).
These need to be evaluated with double integrals.
- Type I: Integrate first over y and then over x. For Example: Evaluating a Double Integral
- Type II: Integrate first over x and then over y. Example: Area Between Curve and y-axis.
References
[1] Austin, A. (2020). Section 15.2 Double Integrals over General Regions. Retrieved May 7, 2020 from: https://www.math.tamu.edu/~austin/Math251_Spring2020_section15_2.pdf
[2] Type I and II regions. Retrieved May 7, 2021 from: https://web.ma.utexas.edu/users/m408s/m408d/CurrentWeb/LM15-3-2.php